Simple Interest

What Is Simple Interest?

Simple interest is the interest earned only on the initial sum of money invested. This initial sum of money is also called the principal amount invested. With this type of interest, interest is not earned on the previously accumulated interest. Instead, it is made only based on the original principle.

Since interest is earned on the original amount invested, a bank account with this type of interest must reach the same interest in each period. Therefore, leaving your money in that bank account will incur the same interest each year.

Another earning interest other than simple interest is called compounding interest. This happens when interest is also made on the previously accumulated interest and the principal amount. 

When accumulated interest is reinvested into a bank account, it is called compounding. This reinvesting will permit the version to earn more and more interest with every period. That is why accounts with compounding interest would gain more interest than ones with simple interest.

This type of interest can also be used when paying back a loan, not only for earning interest from your bank account. Certain loans require the payment of this type of interest, such as:

• Car loans,
• Personal loans,
• Some student loans,
• Short-term, monthly amortized loans.

Loans with simple interest are more beneficial to the borrower. That is because the effect of compounding is not included while paying interest. For the lender, however, compound interest results in them getting more money after repayment.

Understanding simple interest

Before diving deeper into what this type of interest means and how it works, it is essential to understand the concept of future value. The future value is the value of an investment (like a deposit in a bank account) after one or more periods

For example, if a bank account balance will have a worth of $1,000 in one year, it is said that the future value of this investment after one year is $1,000. Future value is how much an investment will be worth at some point in the future.

A sum of money deposited in a bank account will earn interest each period. This means that the future value of this sum of money after one period, for instance, will be greater than the current account balance.

Suppose you invested $1,000 in a bank account that earns 10% interest each year. After one year, the report will have a balance of $1,100. In other words, the future value of this account in 1 year is $1,100. 

After two years, however, it becomes a bit more complicated to calculate the account's future value. That is because, at the end of year 1, the report had a balance of $1,100. So, what should that account balance be at the end of the second year?

Since the bank account only pays interest on the principal, the account's future value at the end of the second year must be $1,200. Interest is earned only on the initial $1,000 invested in the bank account.

In other words, the account earns equal amounts of interest every period. Each year, $100 gets added to the balance as interest. The 10% rate is only rewarded on the principal of $1,000 deposited into the account on day 1. 

Therefore, at the end of year 3, the account would have a balance (future value) of $1,300. At the end of year 4, the bill would have a balance of $1,400, and so on. Yearly interest earned amounts to $100.

Simple interest formula

In the example above, we mentally calculated an investment's future value with simple interest. 10% of the principal, which amounted to $1,000, is $100. Each year, $100 gets added to the account. We just added $1,000 to the total interest earned to find the future value.

However, a formula can ease our calculation of finding the future value of an investment. First, we must go over the procedure of simple interest. This only calculates the interest earned during a certain number of periods.

Simple Interest (S.I.) = P * I * N

• P is the principal amount (initial amount of investment),
• I is the interest rate (can be annual, semiannual, or monthly interest rate),
• N is the number of periods.

The number of periods should be denominated in the same time unit as the interest rate. That is to say, if the interest rate is quoted as a monthly interest rate, then the number of periods must be in months, not years.

For example, if we want to calculate the interest earned on a $4,000 deposit made to a bank account after three years with an annual interest rate of 6%, we use a simple interest formula.

• P = $4,000,
• I = 6% = 0.06
• N = 3 years (we shouldn't change the years to months or half-years since the interest is quoted as an annual interest rate).

Hence,

S.I. = P * I * N = $4,000 * 0.06 * 3 = $720

Therefore, the account has earned $720 in interest throughout the three years. At the end of year 3, the account will have a balance (or future value) of $4,720.

What if the interest rate was quoted as a monthly rate? Suppose we now want to find the interest earned on the $4,000 deposit after three years, but the 6% interest is directly quoted as a monthly interest rate.

• P = $4,000 (same amount deposited),
• I = 6% / 12 = 0.5% = 0.005 (6% annual rate quoted as a monthly rate is equivalent to 0.5% monthly rate since there are 12 months in a year),
• N = 3 * 12 = 36 months (since the interest rate and the number of periods must have the same unit of time, which is months in this case).

Hence,

S.I. = P * I * N = $4,000 * 0.005 * 36 = $720

Notice that the interest earned in both cases is exactly equal. It doesn’t matter if we denote the interest rate monthly or yearly as long as we calculate simple interest.

If the bank account provided compounding interest, then quoting the interest rate as a monthly rate would have rewarded an interest larger than $720. 

That is because the account would have earned interest on the interest accumulated and drawn on the principal.

We can also derive the formula for calculating the future value of an investment that earns this type of interest. Previously, we added the interest earned to the initial principal to find the future value of the investment. Therefore, the formula for the future value of an investment is:

FV = (P * I * N) + P

Using this formula allows us to immediately calculate an investment's future value without calculating the amount of interest it earns. Suppose you deposit $7,500 into a bank account that offers 12%. 

After five years, the account will have a balance (future value) of:

FV = (P * I * N) + P = ($7,500 * 0.12 * 5) + $7,500 = $12,000

Ordinary and exact interest

Ordinary and exact interest are two different types of simple interest. The only difference between the 2 is that calculating common interest assumes a 360-day year (equivalently, 30-day months) while calculating exact interest takes a 365-day year.

Recalling the formula:

S.I = P * I * N

N is the number of periods. It can be denoted in years or fractions of a year. When expressed in months, we convert years to months by multiplying by 12. However, what if N should be said in days? There are two accepted ways of converting years into days:

1. Common interest: we assume that all months are composed of 30 days, so one year is equivalent to 360 days. We thus divide the number of days by 360 to find the number of years.
2. Same interest: we assume that one year is equivalent to 365 days, so we divide the number of days by 365 to find the number of years.

Both methods are viable options for calculating interest earned and future values of investments. However, by default, businesses and banks use the common interest method while calculating the interest they owe on their loans.

The formula for calculating common interest is as follows:

Ordinary Interest = P * I * (D/360)

The formula for calculating exact interest is as follows:

Exact Interest = P * I * (D/365)

Where D is the number of days.

Example Of Common Interest

Suppose you borrowed $1,500 from the bank at an interest rate of 5% for five months. What is the common interest you have to pay in 5 months? Common interest assumes one month to have 30 days and one year to have 360 days. 5 months is equivalent to 5 * 30 = 150 days.

Therefore,

Ordinary Interest = P * I * (D/360) = $1,500 * 0.05 * (150/360) = $31.25

Thus, in addition to paying back the principal, you have to pay an interest of $31.25.

Example Of The Same Interest

Suppose you borrowed $1,500 from the bank at an interest rate of 5% for 150 days. What is the same interest you have to pay in 150 days? The same claim assumes one year to have 365 days.

Therefore,

Exact Interest = P * I * (D/365) = $1,500 * 0.05 * (150/365) = $30.82

Thus, in addition to paying back the principal, you also have to pay an interest of $30.82. Note that by using exact interest, the total interest to be paid is a bit lower compared to the common good. That is because the same claim has five extra days in a year.

Simple interest loans

A simple interest loan is a type of loan that usually comes in the form of a car loan. In this type of loan, interest is paid only on the outstanding principal amount without considering the compounding effect of interest.

The borrower makes equal payments every period when taking out such a loan. One part of the payment is to pay back the principal, and one part is to pay interest on the outstanding principal (the principal left to pay back).

Therefore, with every period, the principal outstanding decreases gradually. Hence, the borrower's interest decreases every month because the amount of principal left to pay is also decreasing. This is why these types of loans are beneficial to borrowers. 

For example, suppose someone borrowed $40,000 to buy a new car. The interest rate on which the person borrows money is 8%. He plans to repay the principal in 5 years. If the person is going to make equal annual payments, she will have to pay $9,732.72.

We found the annual payments to be $10,018.26 by using the following formula:

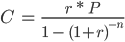
• C is the periodic payment to be made,
• r is the interest rate per period,
• P is the initial principal (the amount borrowed),
• n is the number of periods.

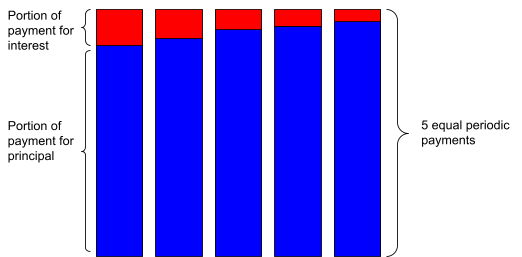
The repayment of the debt will be structured as follows:

1. At the end of the first year, $3,200 will be paid as interest, and $6,818.26 will be paid for the principal.
2. At the end of the second year, $2,654.54 will be paid as interest, and $7,363.72 will be paid for the principal. 
3. At the end of the third year, $2,065.44 will be paid as interest, and $7,952.82 will be paid for the principal.
4. At the end of the fourth year, $1,429.22 will be paid as interest, and $8,589.04 will be paid for the principal.
5. At the end of the fifth year, $742.09 will be paid as interest, and the remaining $9,276.17 will be paid for the principal.

Notice that, with each passing period, a higher percentage of the periodic payment is dedicated to paying back the principal, and a lower portion of the regular price is dedicated to the amount of interest. 

The following image visualizes the idea more clearly.

Researched and authored by Vatche Tchelderian | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Annual Percentage Yield
• Idle Cash
• Key Performance Indicators (KPIs)
• Mezzanine Financing
• Public Companies