PI Function in Excel

What is the PI Function in Excel?

The Pi(π) function in Excel returns the mathematical constant pi value, which is equal to 3.14159265358979.

Pi is one of the most well-known mathematical constants that has puzzled mathematicians for almost 4000 years. 

The first time you are introduced to the concept of π in school is when you are expected to calculate the circumference of a circle using the value of Pi(π) and the diameter. 

So suppose that if the circle's diameter is 10 cm and its circumference is 31.4 cm, what is the value of π? 

π = 3.14159265358979

We are aware that the formula for the calculation of the circumference of the circle is:

Circumference = π x d 

or 

Circumference = 2 x π x r

where,

• r = radius of the circle
• d = diameter of the circle

By rearranging the formula, we get the value of π as:

π = (circumference/ diameter)

    = 31.4 / 10 =3.14

From the calculations, we can deduce that π is the circle's circumference ratio to its diameter. Since circumference and diameter/radius are used in the same unit, π is just a number that does not carry any dimensions.

Understanding the PI function

It is categorized as a Math & Trigonometric function that returns the dimensionless value of the mathematical constant, π, equalling 3.14159265358979 (it is accurate up to 15 digits).

Being an irrational number, Pi has indefinite recurring digits after the decimal. If you're curious, you can see the first 100,000 here. The human brain can't remember all the digits, and a computer can't store them all either, since there are infinite digits. 

The best Excel maintains accuracy up to the first 15 digits in various real-life calculations, such as those for buildings and other architectural structures, quantum physics, medical procedures, and the trajectory of an aircraft in space. 

Here's a great article on how NASA uses the value of Pi in its space adventures.

formula for the PI Function

The syntax for the function is:

=PI()

Where you don't need to add any additional arguments, you begin with the equal sign(=), followed by the function name, and end the formula with parenthesis or round brackets. That's it!

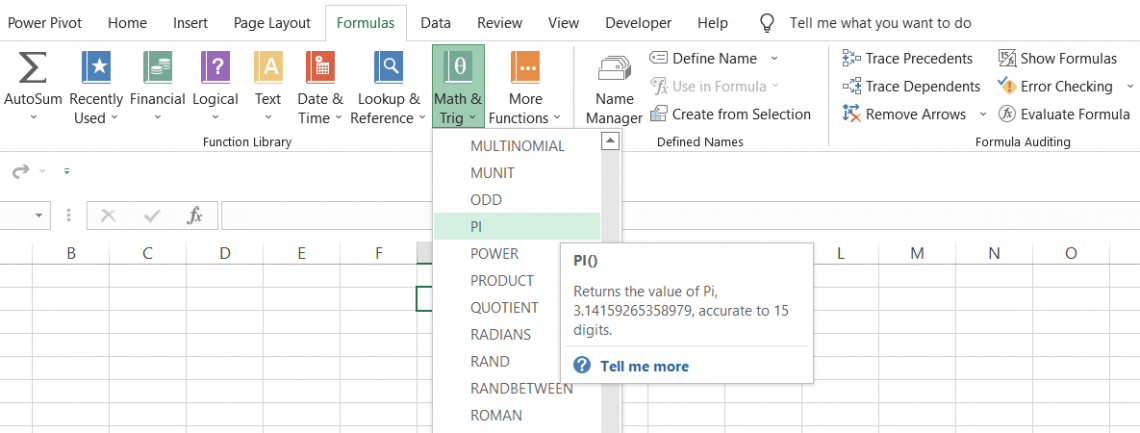
So if you use the formula =PI() in Excel, the result that will be displayed in the spreadsheet will be:

Even though the function returns 14 digits after the decimal point, our spreadsheet only represents six digits. 

To improve the precision of the value, you can either resize the cell's width or increase decimal points using the keyboard shortcut Alt + H + 0. 

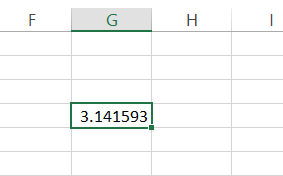
Alternatively, you can select the cell and press Ctrl +1. This will open the Format cell dialog box, where you can set the number of decimal places according to the required result's precision.

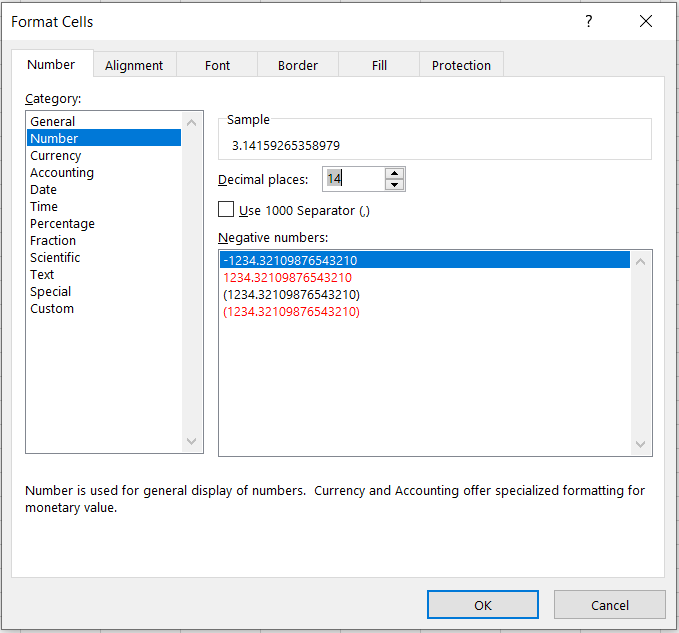
You might notice that once the upper limit of 14 digits is crossed, Excel returns zero for all the decimal increases.

PI Function Example in Excel

There are different instances where you can use this function in Excel. You can use the function while calculating the: 

Circumference of a Circle

Assume that you need to find the circumference of a circle with a diameter of 15 m. Then, the data in Excel looks as illustrated below:

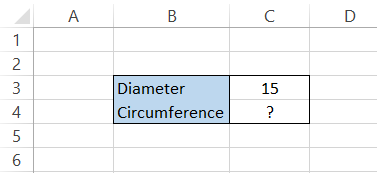
To calculate the circle's circumference, you will use the formula π x diameter or 2 x π x radius. You can either reference the value of π from another cell or directly input it into the formula. 

Let's say we reference the value of π from cell C2. But, first, we will use the function =PI() in cell C2 so that we will get the result:

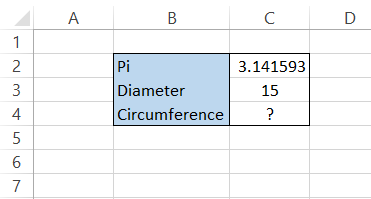
Next, you need to do simple multiplication using the formula C2 x C3 in cell C4 to get the circle's circumference as 47.12389 m.

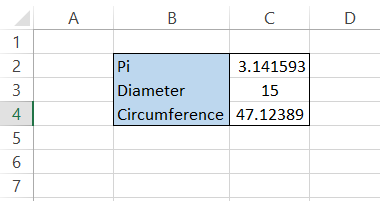
Another method to calculate the circumference is to input the PI function in the calculations directly. 

For example, we will use the formula =C3*PI() in cell C4, giving us the same result as the alternate method.

Area of a Circle

Let's say you need to calculate the circle's area with a diameter of 15 m. The formula to calculate the area of the circle is π x radius². This situation is illustrated below:

First, we find the circle's radius, which is half the diameter. Therefore, the radius in cell C2 will be =C3/2.

Next, we will use the formula =PI()*C2^2, which will give the area of the circle as 176.71 m²

Volume of a sphere

The formula for the volume of a sphere is 4/3 x π x radius³. Assuming that the radius of the circle is 15m, the data is illustrated below:

Here, the radius equals =C3/2, giving the result 7.5m. The formula to calculate the volume of the sphere in cell C4 will be =4/3*PI()*(C2^3) to provide you with the result of 1767.146 m³

Angle degrees into radian

The function can convert the degrees into their radian counterparts. Radians are the standard international (SI) units used to measure angles instead of degrees. 

When an angle of one radian is drawn from the center of the circle, it produces an arc length of 1. The angle that forms is approximately equal to 57 degrees or 1 radian. One degree is equal to (π/180) radians. 

Suppose you need to represent the degrees illustrated below into radians:

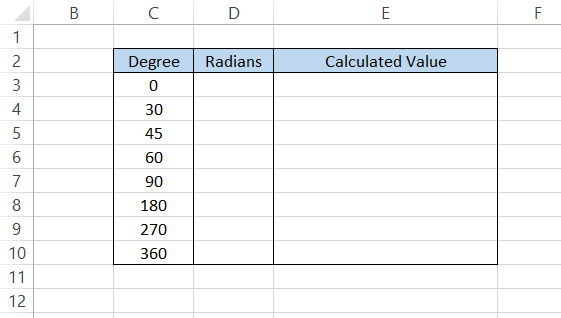
So, if we need to change 30 degrees into radians, the formula will be 30 x (π /180), giving you the result as π/6 (the simplest form of the ratio).

Next, we substitute the value of π, i.e., 3.14159265, using the formula, =PI()/6, which will give you the result as 0.523598776 in cell E4. 

Depending on the value in the denominator, the value of the radian for its degree counterpart will be:

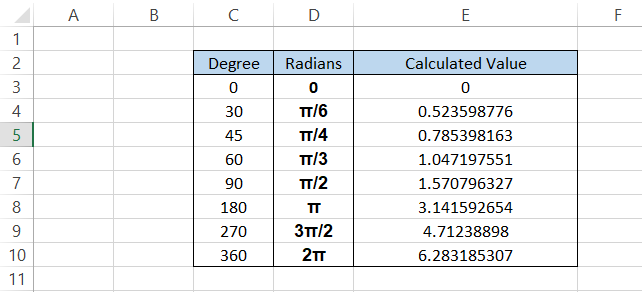
As you can see, the magnitude of one complete revolution of the circle is equal to 2π, which is equal to 2 x 3.14159265, equalling 6.283185307

You can also directly use the formula =C3*PI()/180 in cell E3 and drag it down to the last cell, giving you the same result in the spreadsheet.

Once you understand how radians and degrees work in Excel, you can derive their values using the SIN, COS, and TAN trigonometric functions.

For example, let's say you need to find the value of sin 90°. For this, we will use the formula =SIN(PI()/2), i.e., SIN(π/2), which will give us the result as 1. 

Similarly, you can find the rest of the values by building a table as shown below:

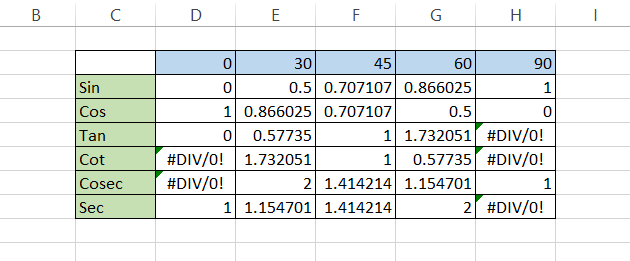
For sin 30°, the result 0.5 can also be represented as ½. Similarly, sin 45° can be represented as 1/2. The formula used to find sin values is equal to =SIN(D2*(PI()/180)), while for cos and tan values it is =COS(D2*(PI()/180)) and =D3/D4 respectively. 

The cot, cosec, and sec functions are the inverses of tan, sin, and cos, respectively (for example, cot = 1/tan).

PI Function Practical Example

Let's say an architect needs your financial advice regarding the construction of a dome-shaped structure on top of a tower. 

The two options would cost $480,000 and $520,000, depending on the size and material (marble, granite, limestone, etc.) used for the dome construction.

The data is illustrated below:

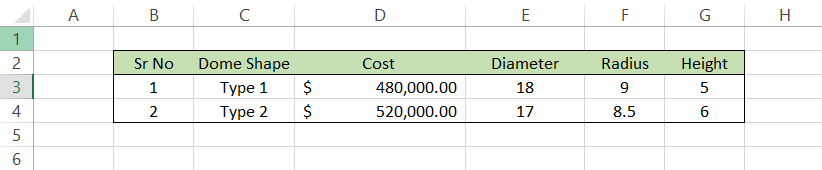
Based on the inputs of both Type-1- and Type-2-shaped domes, the surface area of the dome can be calculated using the formula =ROUND(2*PI()*F3*G3,2), which will give us the result as:

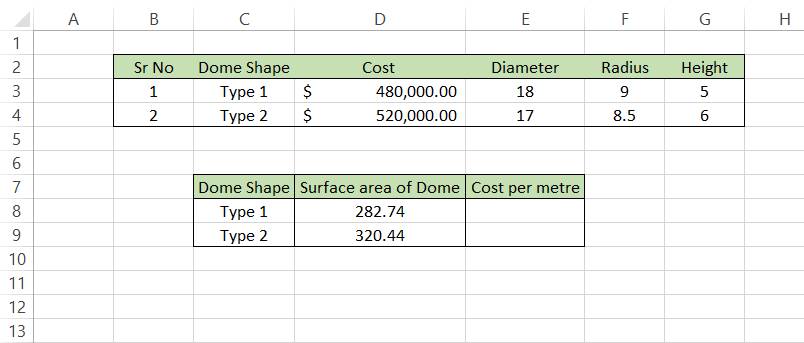
The surface area of the Type 2 dome is equal to 320.44 m2, which is 37.7 m2 larger than the Type 1 dome of 282.74 m2. Finally, we will divide the cost of construction of these domes by the surface area to get the cost per m².

We will use the formula  =D3/D8 in the spreadsheet to get the result:

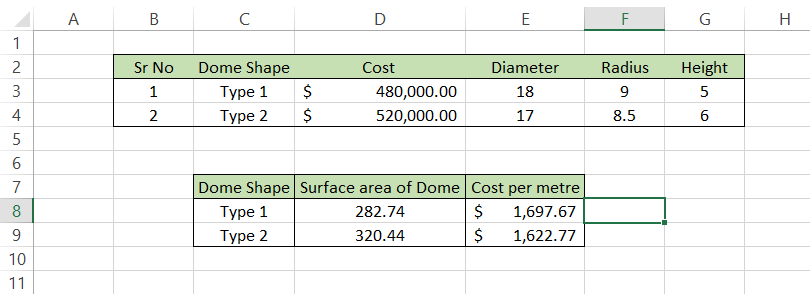
So, by opting for the construction of dome Type 2, the architect can build a structure bigger than the one he would have built with a Type 1. 

If the architect does not need to build a bigger structure, they can substitute the material used for the Type 1 dome and reduce the overall cost.

Conclusion

Excel's PI function is a vital tool that lets users easily and precisely apply the mathematical constant π in their computations.

Thanks to its straightforward syntax and default precision of fifteen digits, the PI function is versatile and can be used in a wide range of applications, from complex scientific investigations to fundamental geometry.

The mathematical importance of π, which denotes the ratio of a circle's circumference to its diameter, is among the most important lessons learned.

Mathematicians have always been fascinated by this irrational number with infinite decimal digits, which has wide applications in a variety of disciplines, including physics, engineering, architecture, and more.

Furthermore, the PI function in Excel may be used for more than just basic calculations; it can be included in intricate formulas to find the characteristics of geometric forms like spheres and circles.

The PI function provides precision in findings and simplifies the process of determining the circumference, area, or volume of various shapes.

Users can make the best decisions possible by evaluating the expenses per unit area of various dome designs in light of their budgetary limitations and project specifications.

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• HYPERLINK Function
• PEARSON Function
• SQRT Function
• STDEVPA Function
• YIELD Function