SQRT Function

What is the SQRT function?

SQRT Function is categorized as a Math and Trigonometry function, it returns the square root of a positive number. Even though the function performs complex square root calculations in a second, it is relatively easy to use with just a single argument you need to input in the syntax.

When you multiply the result of the function by itself, it will give you the number on which you used the SQRT function. 

For example, suppose you must find the square root of numbers from 1 to 100 in Excel. Then, you need to use the said function to give you the result for all the numbers in just a few seconds.

In mathematics, when you find the square root of x to get the result y, the general equation that forms is y = x^1/2. Therefore, this equation can also be represented as y² = x. 

Another interpretation of the equation can be that when y is multiplied by itself, the expected result should be equal to x. For example, the square root of 16 is equal to 4. Also, if we multiply four by itself, i.e., 4 x 4, the result is 16.

Generally, a positive number can return two square roots - one with a positive sign and another with a negative sign. However, if you want to represent the square root with negative signs in Excel, you must add a minus sign (-) before the function.

It does not work when you input negative numbers into the function. We shall see the result later in this article, but it's one of the most important things you must remember before using the function.

SQRT Syntax

Barring some exceptions, most Excel functions have a simple and straightforward syntax that anyone can use and understand. The syntax for the function is:

=SQRT(number)

where,

• number = The numerical value for which you intend to find the square root (required).

This article will guide you on how to use the SQRT function and what other alternatives you can use to find the square roots or the roots for numbers in Excel.

With a bonus VBA section at the end, you can further experiment so that it tells you all the different nth root values with just a single click!

 Example of SQRT Function

Suppose that you need to take the square roots of the number from 100 to 120, as illustrated below:

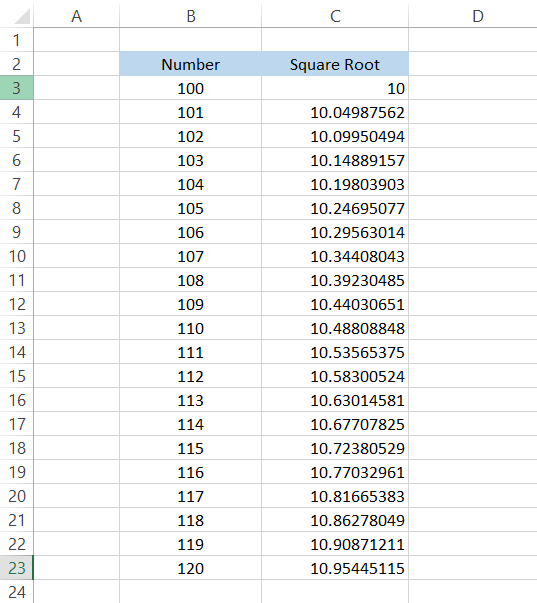
In cell C3, use the formula =SQRT(B3), which will give you the result as 10, i.e., the square root of 100 is 10. Now, drag down the formula to cell C23, and that's it. 

The values in column B correspond to the square roots of the number in column C, as shown:

Imagine how much time it would have taken for you to calculate the square roots of twenty numbers. Try adding a negative sign before the numbers and finding the square root.

Again, we will use the formula =SQRT(B3) and drag it to the last cell. But wait! That's not the result we expected to get in the spreadsheet. 

The said function typically gives a #NUM! Error if the Excel user references or hardcodes a negative value.

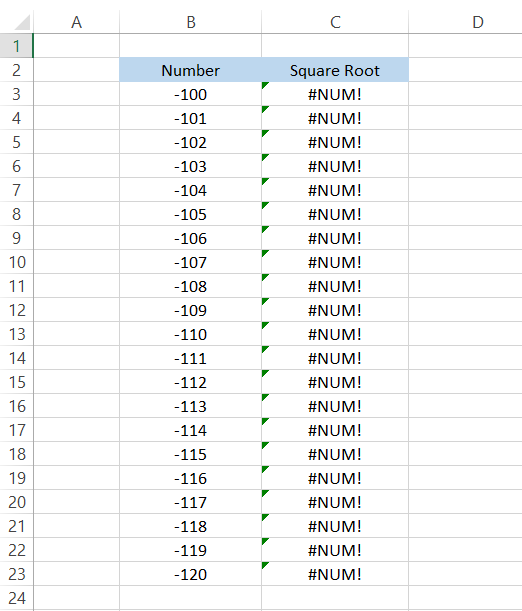
All you need to do to avoid this error is nest the ABS function inside the function. The ABS function returns the absolute value of a number, i.e., it will convert all the negative numbers into positive numbers. 

The only numbers affected by the ABS function are negative, while the positive numerical values remain unaffected.

After the inclusion of the ABS function, the formula becomes =SQRT(ABS(B3)), which will give you the result as illustrated below:

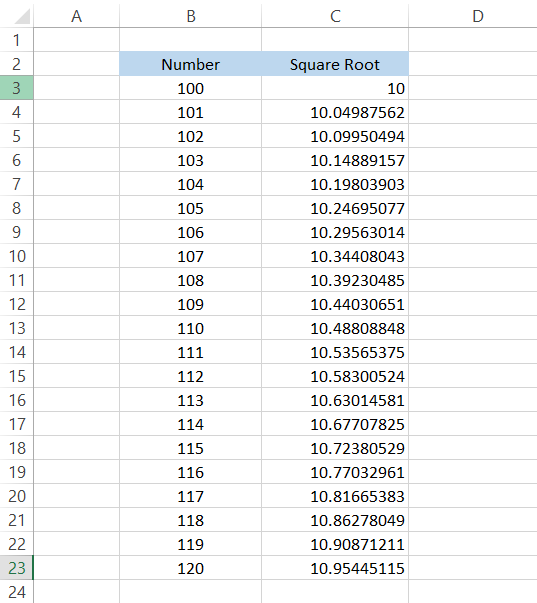
This solves the complications of using negative numbers while finding the square root. 

However, using this function isn't the only method to find the square root of a number. Remember that Excel usually knows how to perform a particular task in several ways, each with its advantages and disadvantages. 

Next, we will see different ways to find a number's square root in Excel.

Finding the square root using manual calculations

If you don't want to use the SQRT function, the other alternative is finding the square root using manual calculations. You might ask, "Why go to such lengths to find the square root?"

Well, to begin with, it sounds complicated, but it absolutely isn't. The function limits you to only finding the square root of a numerical value. But what if you wanted to find the 100th root of a number in Excel?

Excel currently does not have any dedicated function similar to the function to calculate the 100th or even 1000th root of a number, making manual calculations even more important.

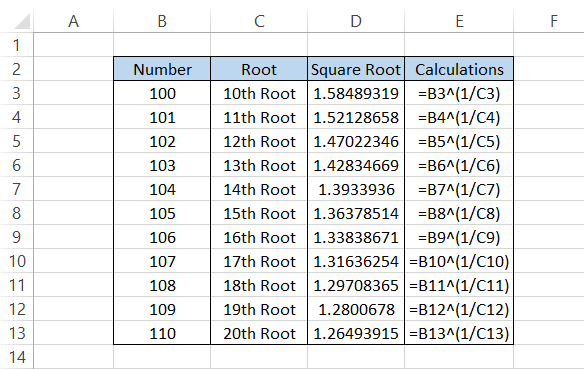
Suppose that you have numbers from 100 to 110 for which you need to find the root values illustrated in column B.

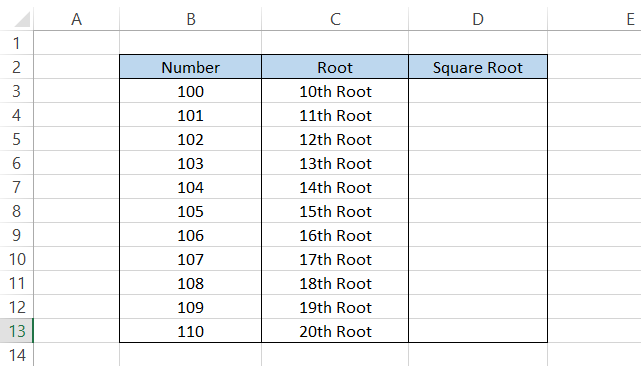
The formula that you will be using in cell D3 is =B3^(1/10) which will give you the result as 1.584893192.

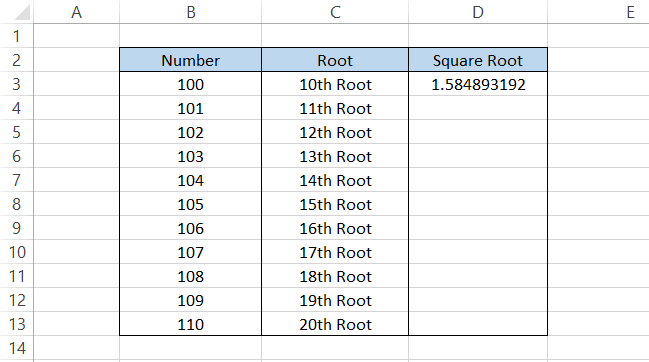
If the number of digits after the decimal point is more than what you expected, you can use the ROUND function that allows you to limit the number of digits after the decimal point. By updating the formula to =ROUND(B3^(1/10),2), you will get the result of 1.58.

Using the caret (^) sign in the formula works similarly to taking power or exponent of a number. So, if you write a formula as 2^2, it will give you the result, 4, similar to finding the square of 2. 

After using the caret (^) sign, we next use the ratio of 1/10. Whatever number root you need to find will always be in the denominator, while one will be constant as the numerator in the formula.

We will make a referenced formula =B3^(1/C3) to drag it down to the last cell. The result you will get is as illustrated below:

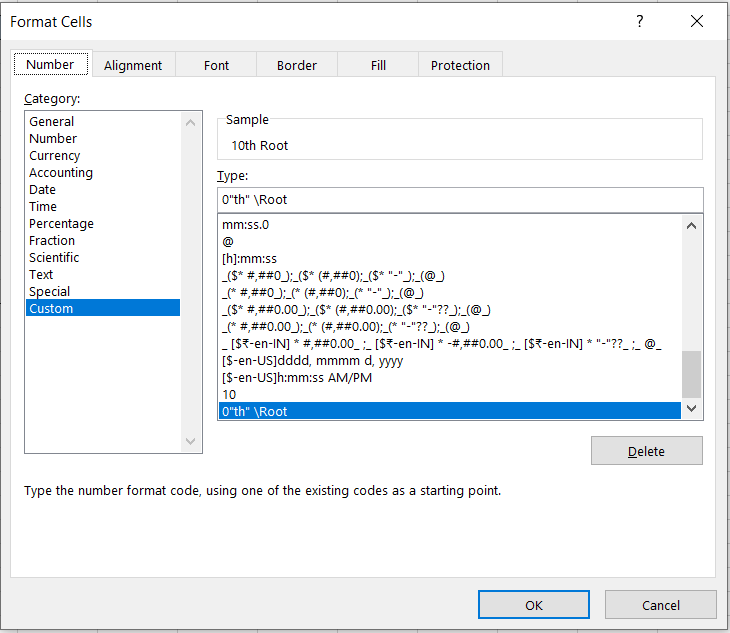
Wait, you might have a question about how we have referenced text in the formula to get the result. We have just reformatted the numbers into those texts. 

The values in column C are still 10,11, 12, 13….20, but you can change them by pressing the Ctrl + 1 key and then using your custom format.

Finding the square root using the POWER function

POWER is another function you can use to find a square root or any other root for a numerical value. The syntax for the function is:

=POWER(number, power)

where,

• number = (required) the base numerical value
• power = (required) the exponent value the numerical value will be raised to.

The POWER function allows you to return both square and square root values based on the power you use in Excel. 

For example, if we have the number 25 and need to find the square root of the number, the formula you will use is =POWER(25,2) and =POWER(25,1/2). This will give you 625 (25 x 25) and five, respectively.

Similarly, you can use different values of power to find the nth root values in Excel, as illustrated below:

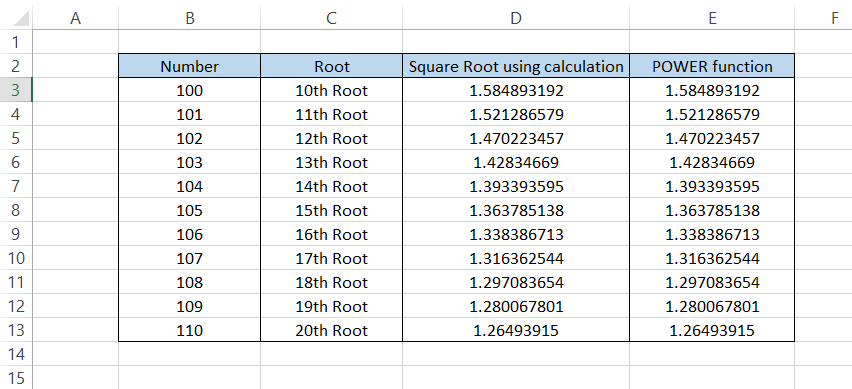
For example, the formula that we have used above in column E is =POWER(B3,(1/C3)).

Finding the square root using a macro

Macros are complicated to make if you do not have a coding background, but they can be quite helpful in improving your efficiency and automating the task flow.

However, coding in VBA is definitely not rocket science. Once you begin learning it, you can master it pretty quickly, as long as you practice. 

Illustrated below is a VBA code that lets you find the square root for the numbers you input in column A. 

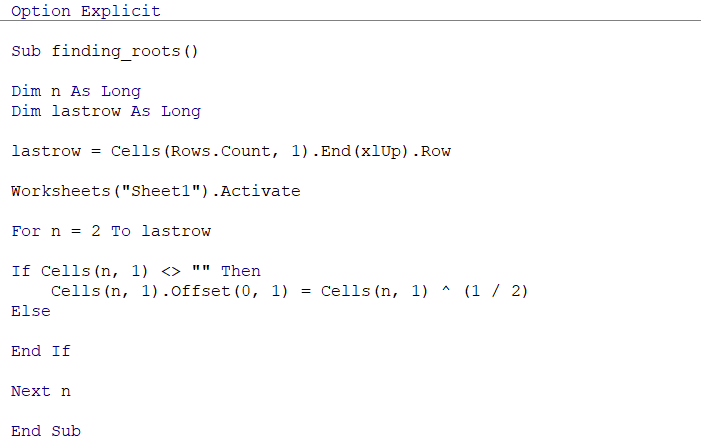
Once you input the numbers, all you need to do is run the code from the developer tab. You will get the result:

Even if you had tens of thousands of numbers, the code would give you the square root in column B. 

However, do note it will only give you the square root. Also, the code will not work if you input the values in any other column than column A. This, however, can be fixed with slight changes to the code provided.

Important things to remember

• You will get a #NUM! Error when you try to find the square root or any other nth root for a negative number in Excel.

• If you find that the result of the SQRT function gives recurring digits after the decimal point, you can use the ROUND, ROUNDUP, and ROUNDDOWN functions.

Researched and Authored by Akash Bagul | Linkedin

Reviewed and edited by James Fazeli-Sinaki | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• COVAR Function
• PEARSON Function
• STDEVPA Function
• VAR.P Function
• YIELD Function