Rule of 72

What Is The Rule Of 72?

The Rule of 72 calculates how many years it takes for an investment to double, given a fixed annual rate of return and interest compounds. The exact compound interest formula is shown below. 

The Rule of 72 is a simple calculation; divide 72 by the annual interest rate, and the quotient is the number of years it will take to double. 

While this calculation is not as accurate as using a formula or Excel, it is helpful to get a quick estimation. Calculating the exact time it takes an investment to double requires a more complex calculation, which cannot be done as fast.

The compound interest formula is harder to use while doing mental math, as it uses algebra/algebra-related skills. 

While 72 is not the only value that could be used, it is the convention to use this number because it is easier to use in a mental math calculation for an approximation. We will explore this idea later in the article. 

Rule of 72 formula and examples

This formula requires the user to divide 72 by the annual interest rate to get the quotient, which is the doubling time. The formula is:

Now, we can look at examples of using the formula: 

Example 1:

Ivy has invested $50,000 into her brother Barry's business. Barry guaranteed her a 7% compounded annual interest rate. How much time will it take for Ivy to double her investment?

First, let's calculate this using the Rule of 72. We must substitute 7 in the equation for the variable r and divide to get t. 

Example 1.1:

t =72 / r

t =72 / 7%

t ≈ 10.29 

The calculated quotient is ≈10.29, meaning it will take Ivy around 10.29 years to double her investment in Barry's business. 

To check the validity of this quotient, we can use the compound interest formula to see if we would get a similar answer. 

We need to substitute:

• 100,000 for A (the total amount at the end)
• 50,000 for P (the principal amount)
• .07 for r (the interest rate as a decimal) 
• 1 for n (the number of times interest is accrued per year)

We need to solve for t to determine the amount of time it takes for this investment to double.

Example 1.2: 

A =P (1+rn)^nt

100,000=50,000 (1+.071)^1t

t ≈ 10.24

After doing the algebra to calculate t, it is found that it will take approximately 10.24 years for Ivy to double her investment. 

While this figure is slightly lower than the 10.29 years we found with the Rule of 72; the values are still very close. 

Example 2: 

Henry has also invested $50,000 into his friend Barry's business. Seventeen years have passed, and his money has doubled. Assuming this is an annually compounded interest rate and has stayed constant in the past 17 years, what is Henry's annual interest rate?

First, let us use the Rule of 72 to help us calculate Henry's interest rate. Then, all we need to do is substitute 17 in for t and solve for r.

Example 2.1: 

t =72 / r

17 =72 / r

r ≈ 4.24% 

By doing this, we find that r is approximately 4.24, meaning Henry's interest rate is 4.24%.

We can also calculate this by using the compound interest equation. 

We need to substitute:

• 100,000 for A (the total amount at the end)
• 50,000 for P (the principal amount)
• 1 for n (the number of times interest is accrued per year)
• 17 for t (the number of years that interest has been accrued)

And we need to solve for r to determine the interest rate that makes this possible.

Example 2.2: 

A=P (1+rn)^nt

100,000 = 50,000 (1+r1)^1*17

r ≈ .0416 ≈ 4.16% 

By using this equation, we now know the interest rate is approximately .0416, or 4.16%. 

This figure is also slightly off from the 4.24% calculated using the Rule of 72, but they are similar values. It is important to note that the 4.16% calculated from the compound interest equation will be more accurate. 

Simple vs. compound interest

The Rule of 72 only works in scenarios of compound interest, not simple interest. So there is a big difference between the two. 

Compound interest is when the investor gains interest in their interest. For example, someone invested $100 at a compounded annual interest of 10%. 

In the first year, they will gain 10% on the $100, so they will get $10 and have $110 in total. In the second year, they will gain 10% on the $110, so they will get $11 and have $121 in total. 

This pattern of gaining interest in the principal and previously-earned interest will continue.

Simple interest is when the investor gains interest only on their principal amount, which is the amount invested initially. 

We will use the same numbers as the compounded interest example for this example to help demonstrate the difference. Someone else invested $100 with a simple annual interest of 10%.

In the first year, they will gain 10% on the $100, so they will earn $10 and have $110 in total.
In the second year, they will gain 10% on the principal (which is $100), so they will receive $10 again and have a total of $120. 

This pattern will continue, with the investor gaining only $10 yearly. 

From these examples, we see that, even though the rates are the same between the simple interest and compound interest investors, the compound interest investor gains more money.

When using simple interest, the yearly gains are the same, but with compound interest, the annual profits grow exponentially. We can see this demonstrated in the graph below.

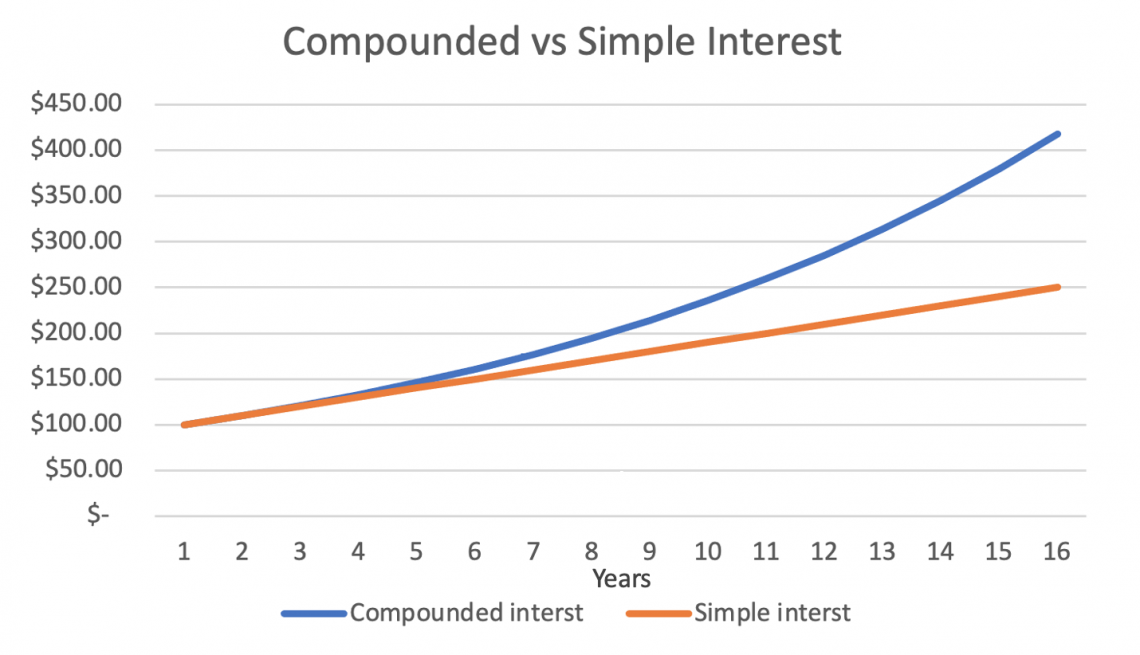
If our example were to continue for up to 16 years, the investor with the compounded interest would have $417.28, whereas the investor with the simple interest investment would have $250. 

These values are far apart, so it is essential to distinguish which type of interest is happening in a scenario and use the appropriate formulas to get the most accurate estimate. 

Rules of 72, 69.3, and 69

While it is called the Rule of 72, 72 is not the only value one may use to check an investment's doubling time. 

The Rule of 69.3 is generally more accurate, as it is the exact value one reaches if one derives the number using a precise formula. 

However, it is trickier to work with as it does not lend itself to being divided when doing mental math. Thus, the Rule of 69 can be used instead of 69.3, as it is a close approximation but can still be easily divided without a calculator. 

Even so, 69.3 or 69 can yield less accurate results as the interest rate increases. We can see this demonstrated in the table below:

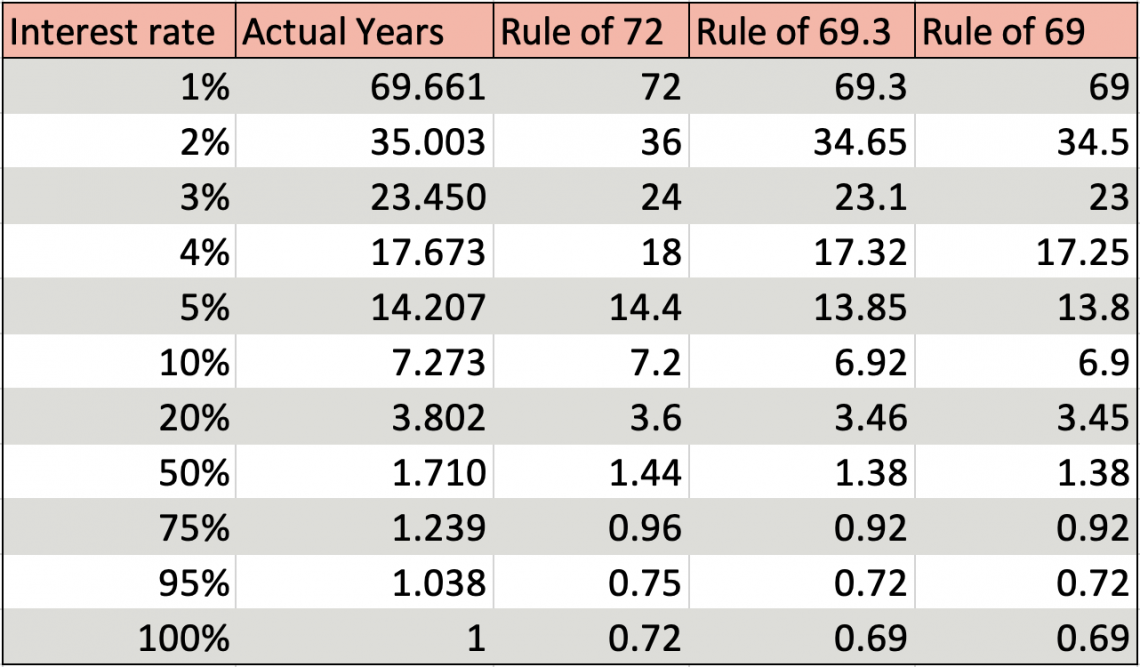
As the interest rate increases, the Rules of 69.3 and 69 get less accurate, and the Rule of 72 gains accuracy. Because 72 is easier to use and is more precise, it is used the most often out of the three. 

Nevertheless, if one knows they are only working with approximating lower interest rates, they may choose to use 69.3 or 69 instead of 72. 

Researched and authored by Divya Ananth | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Day Trading
• Interest Rate Futures
• Relative Strength Index
• Momentum Investing
• Bond Pricing