Time Value of Money
It asserts that money received today is worth more than the same amount received tomorrow.
What Is the Time Value of Money (TVM)?
The time value of money, or TVM, is a fundamental idea in finance. It asserts that money received today is worth more than the same amount received tomorrow.

The reason we say this is quite logical. Any money you have right now can be doubled, tripled, and so on if you choose to invest it. This means you are generating more money in the future following your investment.
This cannot apply to future payments, as you cannot invest in future money now since they have not yet been collected.
Another reason this theory makes sense is that when we talk about future money, money received in the future, there is always the risk that the money may no longer be available. In other words, waiting for future payments instead of collecting a payment now creates a risk factor.
The time value of money can also be called “net present value” or NPV of money.
Let’s say hypothetically; you participated in a raffle competition. You ended up being one of the winners. You are given two options. Your first option (option 1) is to receive a $1,500 prize. Option 2 is to receive the $1,500 in 2 years.
What would your choice be? It is no surprise that most people will choose option 1. One could wonder how option 1 is better if both options give you the same amount.
In support of the fundamental TVM idea, it is much more appealing to collect the money now because there is so much that you can do with it, such as investing.

This proves that the money you can collect now is more valuable than the one you can only collect in two years.
Due to the concept of interest, I could double and triple my money if I make the right investment with the money I collect now (option 1).
Not only is this not possible if I choose option 2, but I also risk losing all of my money due to possible unfortunate circumstances.
Key Takeaways
- The TVM is an idea that explains to us how any money we collect now will be more valuable than the same amount of money we can collect sometime in the future.
- Interest rate and inflation rate are the two main variables we should analyze before we decide on an investment. Both these rates help determine what your expected returns are following an investment.
- The inflation rate has a negative correlation with the TVM, and this is because inflation lowers the value of your currency, meaning that the money you choose to hold will be worth less later.
- The calculation of the TVM involves finding the present amount of money, the FV of that money, how long the money will be invested, and finally, the interest rate. Each of these variables can drastically change the calculated TVM.
- The main positive trait of TVM is that it teaches companies the best ways to make certain business choices. If you think long-term, this results in the company being better positioned.
Time Value of Money and Inflation
Inflation and the time value of money have a negative relationship.

When we discuss investing the money you can collect now, we must consider two things:
1. Interest rate
The Interest rate is important because it will determine how much money you will generate in the future if you choose to invest your present money.
For example, say the annual interest rate is 5%. You have $1,000 in current money that you want to invest.
$1,000 5% is 1000 0.05, equal to 50.
Now we must add the interest we gained to the original amount; we get 1,000 + 50 = 1,050.
If you follow the time value of money principle and collect the $1,000 now, you can invest it and earn more by the end of the year.
In this example, we invested at a 5% rate, giving us a total of $1,050 by the end of the year.
As mentioned above, there is a negative correlation between TVM and inflation.
Inflation has the capability of consistently reducing the value of money, which as a result, will also reduce the purchasing power of your money.
Inflation causes the price of many of the goods we consume to increase. If we deal with dollars, the dollar's value will decrease over time, implying you cannot make as many purchases as you once could.

Knowing this, we must factor in the inflation rate before discussing an investment decision. When calculating an investment's real rate of return, we should always adjust for inflation.
This gives the investor the real return they can generate following an investment, as well as signifying the purchasing power of their money throughout the following years.
In the previous example, we invested our money at the 5% interest rate and made a profit by the end of the year.
Now let’s consider inflation, as we discussed. Say the inflation rate is 10%. This means we must subtract the inflation rate from the interest rate to get the real return value from your investment.
10% - 15% = - 5%. This example shows us how inflation affects the time value of money.
We collected the money and invested it at the 5% interest rate. Still, with inflation, we realize that the value of our money will dip as the inflation rate is higher than our interest rate, thus decreasing our purchasing power yearly.
Present Value Calculation
At the basic level, the idea of present value is quite simple. If you meet your friend today and he gives you $100, the present value would be $100.

Things get a little more complicated when we talk about the present value of a future sum.
Let’s say your friend promises to give you $1,000 next year. What is the present value of that number?
Well, it can't be $1,000 as you don’t have the money in your pocket yet since this is a future payment.
To figure this out, you need to assume that you currently made an investment and that the $1,000 is what you earned as a future amount due to this investment.
As you can probably guess, we need to find out what we had to invest today to reach that $1,000 as a future money payment (next year).
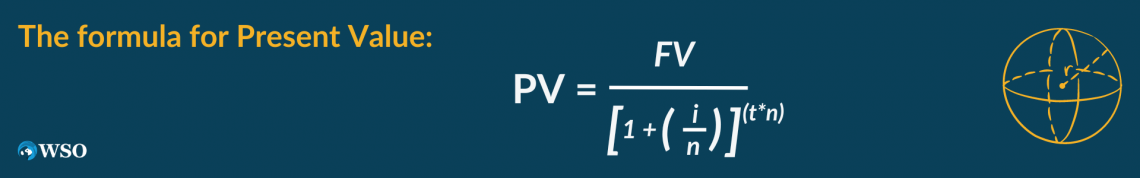
To make this concept easier for ourselves, we can use the formula below to calculate the present value:
Where:
- PV = The present value or current amount
- FV = The future value or the future value of the money you invest today
- i = The interest rate that is given
- t = The number of years we must account for
- n = The number of compound periods we must account for
In the scenario where we are trying to find the present value, we must try to work backward.
We know the future value amount, and we need to imagine how much we need to invest today to reach that future amount later.
Present Value Example
In this example, option 2, your friend owes you money and promises to give you $1,000 in two years.

Option 1 you demand and receive the $1,000 now so you can invest it in stocks or real estate.
To understand the importance of present value, let’s choose option 2.
Since we are working backward, we must subtract the total earnings generated from the interest rate by our base number of 1,000.
We essentially have to discount (by the interest rate) the money back two years, as stated in option 2.
Assume the interest rate is 5% and the number of compound periods is 1. Let’s plug them into the formula we showed above:
PV = $1,000 / [1 + (5% / 1)] (2x1)
PV = $907.02
This leads to a present value of $907.02.
This calculation showed us that the PV of the $1,000 cash you will receive in two years equals $907.02, assuming the interest rate is still 5% for the next two years.
Now we have the full picture when it comes to option 2. We can conclude that if we chose option 2, it would be as if we were receiving $907.02 now and using that money for some type of investment for the next two years.
If we bring this back to the topic of the time value of money, also known as the present discounted value, our example proves that the theory stands correct.
This is because if you compare options 1 and 2, you can see the difference in the starting base value that a potential investor can have.
In the first option, you can collect the $1,000 now (base money) from your friend and then invest it in generating a higher return for the next two years.
In the second option, we used the present value calculation and determined that if you were to collect the $1,000 two years from now, it would be as if you are receiving $907.02 now (base money) and then using them for investment for the next two years.
This means that, in support of the TVM theory, option 1 is better for you because you can start with a higher value now, which means if you choose to invest that money, you will also generate a higher return in two years.
Future Value Calculation
In other scenarios, we will try to find a payment's future value instead of the present value.

Finding future value is important as it gives companies insight into making important business decisions.
TVM can help them determine whether to invest in a certain product or buy a certain asset. To help you understand the concept of future value, let’s say you were given $2,000 to spend by your parents.
You decide to generate at least double that amount to buy something you like and invest the money.
If you invest that money at the 5% interest rate, for example, in one year, you will earn $2,100.
We got this by multiplying 2,000 by 5%, which gave us 100. Add 100 to the original number; you get 2,100.
Let’s say you want to keep investing your money for another year. We can follow the same steps.
$2,100 multiplied by 5% gives us 105. Add 105 to 2,100 you get $2,205 as money generated through investment by the end of the second year.
As you can see, it is easier to use a formula as we continuously invest our money.

Using the present value equation above, we can manipulate the equation to find the future value. This is what we get:
Where:
- PV = The present value or current amount
- FV = The future value or the future value of the money you invest today
- i = The interest rate that is given
- t = The number of years we must account for
- n = The number of compound periods we must account for
Future Value Example
In this example 1, we will see how we use TVM.

Let’s say we have $150,500 (present value) in our bank and want to invest the money every year for five years. The interest rate will be 15%. Assume the number of compound periods is just one. The future value calculation will be:
FV = FV = $150,500 * [1 + (0.15 / 1)] (5*1)
FV = $302,709.25
This means that the future value, FV of the money we used to invest, will be worth $302,709, more than double our original amount.
Example 2: Finally, let's look at another example, but this time the compound period is more than just one.
Suppose we have $25,000 (present value) in cash, and we would like to invest them for three years in hopes of future great returns.
The annual interest rate is 3.5%, and the number of compound periods is now two. Let’s calculate the FV using the same formula as above:
FV = $25,000 * [1 + (0.035 / 2)] (3*2)
FV = $27,742.55
The future value of the $25,000 we invested will be $27,742.55.
This example proves that we must pay attention to the compound periods because the TVM can change drastically depending on the number of compounding periods in the equation.



or Want to Sign up with your social account?