Laspeyres Price Index

Author:

Reviewed By:

Last Updated:December 13, 2023

In This Article

What Is The Laspeyres Price Index?

A consumer pricing index called the Laspeyres Price Index is used to track price changes for various goods and services concerning a predetermined base period weighting.

German economist Etienne Laspeyres created LPI, also known as the base year quantity weighted technique.

It is a price index that helps gauge inflation rates, the general price level, and the economy's cost of living.

A base year value of 100 is usually used for the index, with periods of higher price levels represented by an index larger than 100 and periods of lower price levels by an index lower than 100.

The fact that the Laspeyres index employs weights derived from a base period sets it apart from other indexes such as the Paasche Price Index, Fisher-Price Index, etc. It provides a solution to the issue of how much a basket of goods that customers purchased in the base period would cost in the present.

Key Takeaways

The Laspeyres Price Index tracks price changes using a base year value of 100, with values above 100 indicating price increases.
Laspeyres Price Index helps measure inflation rates and the cost of living in the economy.
Laspeyres Price Index uses base period weights and doesn't require current period basket data, making it practical for quick economic analysis.
Economists use this index for policy-making and economic analysis, but it may not represent individual spending patterns accurately.

Understanding The Laspeyres Price Index

Laspeyres Price Index describes a fixed-weight or fixed-basket, an index that uses the base period's weighted average of the basket of goods and services. A "base-weighted index" is another name for it.

Other price index formulae may be used in price statistics, such as the Paasche price index, Fisher-price index, etc.

However, the choice of the index formula frequently depends on the data's accessibility. The Laspeyres index does not require knowledge of the current period's basket, contrary to the other algorithms.

Since consumer price indices are built and disseminated quickly before consumption or production data for the current period is gathered, the Laspeyres method is typically brought into practice.

Therefore, in a nutshell, we can say:

The base year for the index analysis is generally 100. A price increase is indicated by an index over 100, and a price decrease by an index below 100.
The base year is year 0, and the calculation year is the duration of the observation year.
When analyzing the nation's economic growth, economists increasingly consider the inflation of commodities and services.

Formula For The Laspeyres Price Index

The formula for the Laspeyres Price Index is as follows:

LPI

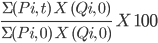
Where:

The prices of the individual items at the base period and observation period are represented by Pi,0 and Pi,t, respectively
The amount of each item during the base period is Qi, 0

The mathematical notations are not to be misunderstood.

The total expenditures for all items during the observation period in base amounts make up the numerator, while the total expenditures for all items during the base period in base quantities make up the denominator.

Consequently, the following rewriting of the Laspeyres Price Index makes it easier to understand:

Laspeyres Index Formula= ∑(Observation Price * Base Qty) / ∑(Base Price * Base Qty)

Where

Observation Price: The price at the present levels for which the index must be constructed
Observation Quantity: The quantity at the present values for which the index must be determined
As the basis year for computing the index, year 0's price is referred to as the Base price.

Applications of the Laspeyres Price Index

This section explores the various ways in which LPI is employed for practical purposes, such as:

1. Inflation Measurement

The primary role of the Laspeyres Price Index is to measure inflation accurately.

By tracking changes in the prices of a fixed basket of goods and services relative to a base period, LPI calculates inflation rates with high accuracy, ensuring precise measurement vital for economic analysis and policymaking.

For policymakers and central banks, understanding inflation is essential for making informed decisions about monetary policy. LPI allows them to monitor price movements within the economy, identify inflationary or deflationary trends, and take timely actions to stabilize the economy.

Note

Accurate inflation data is crucial for adjusting interest rates, managing currency values, and ensuring economic stability.

2. Cost of Living Analysis

The index helps determine how much more or less it costs for individuals or households to maintain their standard of living over time.

For example, if the LPI indicates that the cost of the fixed basket of goods and services has increased compared to the base period, consumers may find it more expensive to afford the same items they purchased previously.

This insight is essential for individuals and families to make informed financial decisions, plan their budgets, and adapt their spending habits to changing economic conditions.

3. Economic Analysis

Economists rely on the Laspeyres Price Index as a vital tool for conducting comprehensive economic analysis. It allows them to explore various economic trends and phenomena, providing valuable insights into the health of an economy.

Here's how economists utilize the index for economic analysis:

Tracking Consumer Behavior: LPI helps economists study how consumers respond to price changes.
Comparing Economic Performance: Economists use LPI to compare economic performance across regions, industries, or time periods.
Policy Formulation: Policymakers use LPI data to shape economic policies.

Laspeyres Price Index Advantages

By comparing the current price levels with the amount from the base year, the Laspeyres Price Index is a vital tool in economic analysis and offers a comprehensive perspective on price movements within an economy.

These advantages, while notable, should be considered alongside the index's inherent drawbacks for a more balanced understanding of its utility in assessing price dynamics.

Here are some key advantages:

Calculations on an Excel spreadsheet are fairly simple.
There is no need to compute the amounts for future years because it simply considers base-year quantities and current-level pricing.
Since it uses base year numbers and disregards the quantities at the current, it provides a realistic representation and value of the commodities.
Future inflation-controlling strategies are framed using this criterion.
Both calculating and comprehending it are easy.
Due to the data's accessibility, it is affordable.
Because it just utilizes the values from the base year, one need not compute the amounts for subsequent years.
Due to its consideration of base year amounts, this index reasonably represents the commodities' worth.
Because a change in the index corresponds to a change in the price, it provides a useful comparison.
The index's results help create policies to control inflation.

Laspeyres Price Index Disadvantages

While the index has several advantages, it is important to acknowledge its disadvantages and limitations in the field of economic analysis and price measurement.

These drawbacks often necessitate the consideration of alternative indices for a more accurate and comprehensive assessment of price changes.

Here are some key disadvantages:

This indicator could exaggerate the rate of price growth.
The amounts in the current year or the observation year are not considered.
The expanding economy is not considered in this measure. Additionally, it makes no allowance for changes in output levels over time. Further, it ignores brand-new competitors.
The existence of replacement items and changes in product quality are additional factors that this index does not consider. The consumption pattern may alter because of changes in the quality and accessibility of replacement items. Therefore, it may have a significant effect on commodity prices. In that sense, the index might not accurately depict the situation.
Finalizing the base year might be challenging.
As of now, the quantity levels are not considered.
Ignoring the quantity levels will result in incorrect results in the model since production levels may alter in the coming years.
It utterly disregards the recent market entries.
The substitution of items and changes in quality, which can significantly affect pricing, are not considered.
When replacing products, outdated models may raise the price to manufacturing levels. Therefore, excluding future numbers will result in an incorrect index figure and possess an immediate effect on future government policy.

Laspeyres Index and Upward-bias

Laspeyres Price Index's major flaw is that it has an upward tilt and could exaggerate price increases. As a result, it could potentially overstate inflation and price levels. The following three causes might account for this upward bias or overstatement of price increases:

Any quality enhancement may result in a rise in a commodity's price. Such a price increase should not be viewed as inflation.
Individuals often replace items that have increased in price with substantially less expensive ones.
The gradual replacement of older products with more expensive new ones.

We may say that consumers alter their purchasing habits and preferences as prices increase. When a commodity's price increases, consumers begin to purchase less amount of that commodity and more of those goods with little or no price change.

The selection of base-year commodities may therefore overestimate the decline in the quality of living and inflation if the overall satisfaction level does not decrease.

The progressive substitution of more expensive new items for older ones is the third factor contributing to an upward bias.

Therefore, if the degree of overall happiness does not diminish, the choice of base-year commodities may exaggerate the loss in living standards and inflation.

The government will respond to a large shift in the price index by enacting new market-clearing regulations, which will lessen the impact of rising prices on the general population.

Example of Laspeyres Price Index

To comprehend how the Laspeyres Price Index for commodities A, B, and C is calculated, let's look at the example below.

Commodities: prices and quantity
Prices	A	B	C	Quantity	D	E	F
Commodity	Year 0	Year 1	Year 2	Commodity	Year 0	Year 1	Year 2
A	10	25	40	A	10	15	20
B	15	30	45	B	20	25	30
C	20	35	50	C	30	35	40

The numbers for the following years are not necessary to compute the Laspeyres Price Index in the example above; they have not been shown in the table. The procedures for calculating the index are, nevertheless, listed below.

As of year zero, the Laspeyres Price Index is 100. Since the numerator and denominator are the same in this calculation, the base year result would be 100.

This value will be used in subsequent years to compare the performance of the goods and services and to develop a suitable action plan in the event of an excessive price increase or decrease that would directly impact consumers and the economy.

Calculation at Year 1 will be:

Laspeyres Index Formula= ∑(Observation Price * Base Qty) / ∑(Base Price * Base Qty)

{(25 * 10) + (30 * 20) + (35 * 30)} / {(10 * 10) + (15 * 20) + (20 * 30)} = 190

Index at year 1 = 190

Calculation at Year 2 will be:

Laspeyres Price Index formula for year 2 = {(40 * 10) + (45 * 20) + (50 * 30)} / {(10 * 10) + (15 * 20) + (20 * 30)}

Index at year 2 = 280

Thus, we can see how inflation has affected prices as the cost of goods has gone up because prices grew from 100 to 190 in year one to eventually 280 in year two.

Conclusion

One of the most often used price indices for determining how much a basket of products and services has changed over a certain base period is the Laspeyres Price Index.

The total expenditures for all items during the observation period using base period quantities make up the index's numerator, while the total expenditure for all goods using base period prices and quantities make up the denominator.

This is one of the important ratios to gauge how quickly prices for products and services are rising. The Laspeyres price index employs base year amounts, unlike the Paasche price index, which uses current level numbers in its calculation.

As a result, the two cannot be compared and will provide entirely distinct images of price changes.

Economists have heavily exploited this index to influence the consumer market and the nation's finances without subjecting the general populace to the strain of rising prices.

This indicator is frequently used by economists and decision-makers to develop financial and economic policies that will benefit society.

The government uses the Retail Prices Index (RPI) and Consumer Prices Index (CPI) to gauge inflation. Each month, a Laspeyres index is derived from the total cost of a predetermined "basket of goods and services" under each scenario.

By revising the basket of goods and services each year, changes in spending patterns are accommodated. The CPI and RPI, however, might not be a reliable indicator of how changing prices affect you since different individuals spend their money differently.

You may create a personal fixed base Laspeyres index by keeping track of the costs and quantities of the items you frequently purchase to determine how inflation impacts you specifically.