Annuity Due
It is a stream of equal cash flows that occur over a given period at the beginning of each interval
What is Annuity Due?
An annuity due is a stream of equal cash flows that occur over a given period at the beginning of each interval; receiving $100 per year at the end of each of the next five years is an example of an annuity.
There are two types of annuities: ordinary annuity and annuity due.
The most common type of annuity is the ordinary annuity. Cash flows characterize it at the end of each compounding period. This is a typical cash flow pattern for many investment and business finance applications.
The other type of annuity is an annuity due, where payments or receipts occur at the beginning of each period i.e., the first payment is today at t = 0.
An example of an annuity due payment is the rent paid at the beginning of each month. And an example of an ordinary annuity includes utility bills and loans, such as mortgages.
Key Takeaways
- An annuity due involves regular payments at the beginning of each interval, contrasting with ordinary annuities where payments occur at the end of each period.
- Annuities due have legal implications as payments received represent assets, while those making payments have debt liabilities.
- The key difference between annuity due and ordinary annuity lies in payment timing.
Relevance and Use of Annuity Due
It requires the payments made at the beginning of each period instead of the end of each annuity period.
The payments received by an individual through annuities due legally represent an asset (rent paid for the following month). At the same time, the individual paying the annuities due has a legal debt liability requiring periodic payments (for example, EMI payments).
One can use present value/future value calculations because a series of annuities' due payments reflects several future cash inflows or outflows.
The recipient or payer of the funds may wish to find out the entire value of the annuity at the end of the period (future value)/ beginning of the period (present value) while factoring with the time value of money.
For example, a company enters into an office lease, under which the lessor requires the company to make monthly payments of $10,000 for the next 36 months before the beginning of the month.
Since all payments are of the same amount ($10,000), these payments are annuity due as the payments are made at regular intervals (monthly), and the payments are made at the beginning of each period.
Annuity Due vs. Ordinary Annuity
An annuity due is a recurring payment of money at the beginning of a period (first day of a week/month/quarter/year).
Alternatively, an ordinary annuity is a recurring payment of money at the end of a period (last day of a week/month/quarter/year).
Business agreements and Contracts outline this payment method, and it is based on when the benefit is received.
I.e., When paying for an expense, the beneficiary makes ordinary annuity payments after the benefit has occurred, while the beneficiary pays annuities due payment before receiving the benefit.
The timing of an annuity payment is based on opportunity costs.
The payment collector may invest the annuities' due payment to generate interest or capital gains. As they have the opportunity to use funds faster, this is the reason why it is more beneficial for the recipient.
Those individuals paying annuities tend to prefer ordinary annuities as they will lose out on the opportunity to use the payment funds for an entire period.
Calculating Annuity Due on a calculator
Although there are formulas to calculate the Present Value (PVAD) and Future Value (FVAD) of Annuity Due, it is highly recommended to use a calculator.
Using a calculator not only saves time but also helps in reducing the probability of making errors while calculating manually.
The calculator used here is Texas Instruments BA II Plus.
Question Annuity due with
- A = 10
- r = 5%
- N = 5
Here,
- A stands for Annuity (Payments- PMT)
- R stands for rate of interest (I/Y)
- N stands for Number of years
- PV stands for Present Value
- FV stands for Future Value
| Key Strokes | Display |
|---|---|
| [2nd] [BGN] [2nd] [SET] | BGN |
| [2nd] [QUIT] | BGN 0 |
| [2nd] [CLR TVM] | BGN 0 |
| 5 [N] | BGN N = 5 |
| 5 [I/Y] | BGN I/Y = 5 |
| 10 [PMT] | BGN PMT = 10 |
| 0 [FV] | BGN FV = 0 |
| [CPT] [PV] | BGN PV = 45.45 |
| 2nd] [BGN] [2nd] [SET] | END |
| 2nd] [QUIT] | 0 |
Present Value of an Annuity Due
While less common than those for ordinary annuities, some problems may require you to find the PV of an annuity due (PVAD). However, using a financial calculator like the Texas Instrument BA II Plus financial calculator should not be much of a problem.
With annuity due, there is one less discounting period as the first cash flow occurs at t = 0, which is already its Present Value.
This implies that (all else equal) the Present Value of an annuity due will be greater than the Present Value of an ordinary annuity.
As you will see in the example, there are two ways to compute the PV:
- The first way is to set the calculator in the BGN mode and then input all the relevant variables (PMT, I/Y, and N) as we usually would.
- The second is a far easier way, i.e., to treat the cash flow stream as an ordinary annuity over N compounding periods and multiply the resulting PV by [1 + periodic compounding rate (I/Y)].
Symbolically, this can be expressed as
PVAD = PVAO × (1 + I/Y)
The advantage of the second method is that we can leave your calculator in the END mode and will not have the risk of forgetting to reset the modes. Regardless of the procedure used, the computed Present Value is given as of the beginning of the first period, t = 0.
The following examples illustrate how to compute the PV.
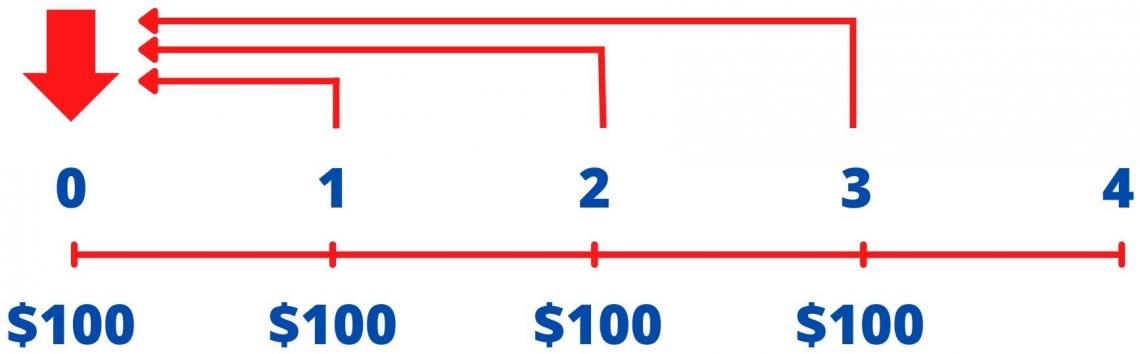
Example: Given a discount rate of 10%, what is the PV of an annuity that makes $100 payments at the beginning of each of the next four years, starting today?
Answer: First, this problem can be solved using the Calculator's BGN mode. Set the calculator to the beginning (BGN) mode: ([2nd] [BGN] [2nd] [SET] [2nd] [QUIT] or [g] [BEG] on the HP) and enter the relevant data, and compute PV.
N = 4; I/Y = 10; PMT = –100; CPT → PVAD = $348.68
The timeline for this problem is shown in the following figure.
Alternatively, this problem can be solved by leaving the calculator in the END mode. First, compute the PV of an ordinary four-year annuity. And then multiply this PV by (1 + I/Y). To use this approach, enter the relevant inputs and compute PV.
N = 4; I/Y = 10; PMT = –100; CPT → PVAO = $316.98
PVAD = PVAO × (1 + I/Y) = $497.37 × 1.10 = $348.68
Future Value of an Annuity Due
It is necessary to compute the Future Value of an annuity due (FVAD), i.e., an annuity where the payments or deposits occur at the beginning of each period (compounding period).
Fortunately, the Texas Instrument BA II Plus financial calculator can be used to do this. Still, with one slight modification—the calculator must be set to the beginning-of-period (BGN) mode.
To switch between the END and BGN modes on the Texas Instrument BA II Plus, press the following keystrokes—[2nd] [BGN] [2nd] [SET]. When this mode is set, "BGN" will appear on the upper right corner of the display window screen.
If the display indicates the desired mode, press [2nd] [QUIT] keystrokes.
You will generally want your calculator to be in the ordinary annuity (END) mode, so remember to switch out of BGN mode after working annuities due to problems.
Note
Nothing will appear on the upper right corner of the display window screen when the Texas Instrument BA II Plus financial calculator is set to the END mode.
While these payments are received or made at the beginning of each period, the Future Value of annuities due is calculated at the end of the last period.
Another way to compute the Future Value is to calculate the Future Value of an ordinary annuity and multiply the resulting Future Value by [1 + periodic compounding rate (I/Y)].
Symbolically, this can be expressed as
FVAD = FVAO × (1 + I/Y)
The following example illustrates how to compute the Future Value.
Example: What is the FV of an annuity that pays $100 per year commencing today, at the beginning of each of the next four years, if the cash flows can be invested at an annual rate of 10%?
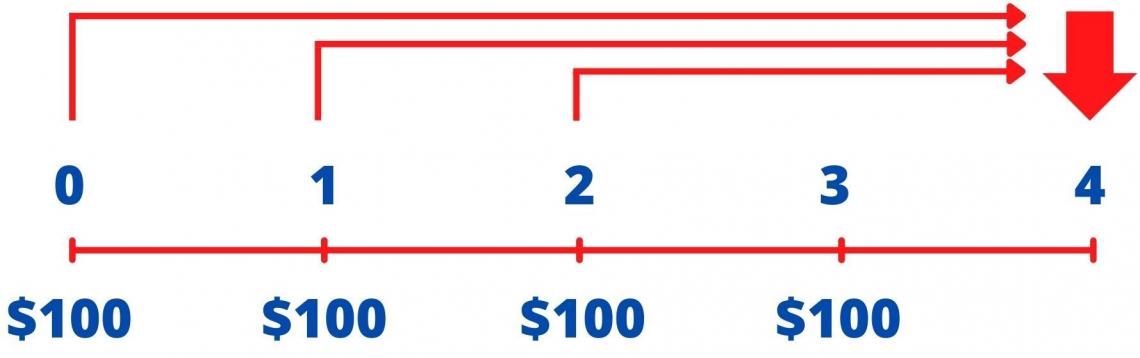
Answer: Note in the timeline in the following figure that the FV is computed as of the end of the last year in the annuity's life, i.e., Year 4, even though the final payment will occur at the beginning of Year 4 (end of Year 3).
To solve this, put the calculator at the beginning (BGN) mode:
([2nd] [BGN] [2nd] [SET] [2nd] [QUIT] or [g] [BEG] on the HP), and then input the relevant data and compute the Future Value.
N = 4; I/Y = 10; PMT = –100; CPT → FV = $510.51
Alternatively, we can calculate the Future Value for an ordinary annuity and multiply it by (1 + I/Y). Leaving the calculator in the END mode, enter the following inputs:
N = 4; I/Y = 10; PMT = –100; CPT → FVAO = $464.10
FVAD = FVAO × (1 + I/Y) = 464.1 × 1.10 = $510.51
The $728.20 computed here represents the amount of money that an investor would receive by the end of the second year/ beginning of the third year.
Annuity Due FAQs
Yes, Income payments from an annuity are taxed as ordinary income.
The answer depends on whether you are the payer or payee.
As a payer, an ordinary annuity might be preferable as it makes the payment at the end of the period rather than at the beginning of the period. With these funds, the payer can use those funds for the entire period before paying.
As a payee, an annuity due might be preferable because the payment is received upfront at the beginning of the period, allowing the payee to utilize the funds immediately and enjoy a higher present value than it offers in comparison to that of an ordinary annuity.
Often, an individual does not have the option to choose.
For example, Life Insurance premiums are an example of annuities due, with premium payments due at the beginning of the covered period. A car EMI payment is an example of an ordinary annuity, with payments due at the end of the covered period.
Perpetuities are annuities with infinite lives (perpetual annuities). In Simpler Terms, a perpetuity is a financial instrument that pays a fixed amount of money at set intervals over a finite period. In essence, a perpetuity is a perpetual annuity.
Most preferred stocks are examples of perpetuities since they promise fixed interest or dividend payments forever.
Without going into all the mathematical details, the discount factor for perpetuity is just one divided by the appropriate rate of return (i.e., 1/r).
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:


or Want to Sign up with your social account?