Discount Factor

What is the Discount Factor?

 A discount factor is a number that is derived from the discount rate. It represents the value of $1 discounted back to the present at the specific discount rate.

It is usually a decimal value that can be used as a multiplier to discount a future cash flow back to its present value. It is not very far removed from its cousin the discount rate.

In fact, the discount rate is used to calculate the discount factor, and hence they are very closely related. Therefore, it is a valuable tool for taking into account the time value of money and is often used while valuing an investment.

The discount rate may be calculated in several ways. However, it usually represents the minimum required rate of return on investment, especially when used to calculate its net present value (NPV).

For example, the minimum required rate of return for a company could be its cost of financing. Let’s assume that a firm's weighted average cost of capital is 10%. If the firm generates only 5% on its investments, it is making a loss as it can’t pay back the 10% WACC. Hence in most cases, WACC is used as a proxy to the discount rate.

Another method involves using a benchmark rate, one that a company uses to filter out investments that don’t make a sizable profit.

There is no shortage of ways to calculate an appropriate discount rate, which are all meant to reflect the time value of money.

The discount factor is most commonly used in a discounted cash flow (DCF) analysis, an intrinsic method of analysis that measures the profitability of an investment and considers the time value of money.

Discount Factor Formula

The discount factor is closely related to the discount rate. They are both used within discount cash flow (DCF) analysis and largely serve the same purpose. The discount factor shows the effect of the time value of money on a dollar to be received in the future.

This concept represents the idea that money now is worth more than money later because money in the present can be used to invest, creating a greater return in the future. Inflation also plays a role in the time value of money because as time passes, money will slowly lose its value due to inflation. Future cash flows that are discounted to represent their current value are called a money’s net present value (NPV).

The discount factor can be calculated using the discount rate as follows:

DF = 1 / (1 + DR)^T

where,

• DF = discount factor 
• DR = discount rate 
• T = number of years

Once the discount factor is calculated, it can be multiplied by any cash flow in the given year to yield the cash flow’s NPV. It is important to note that the discount factor decreases in relation to time.

It is only logical because as the number of years to receive the money increases, the lesser its present value.

What is the Discount Rate

As we saw from the discount factor formula, the discount rate plays a key role while calculating it. A discount rate can either be used directly or through the discount factor while calculating the NPV.

The equation to calculate the NPV from the discount rate is given below:

NPV = CF / (1 + DR)T

where,

• CF = cash flows
• DR = discount rate
• T = years

This equation may look incredibly similar, and it should. It is essentially the same formula that is used to find the discount factor. While calculating the discount factor, we use $1 of cash flow in the formula.

Discount Factor Example

The discount factor may be multiplied by future cash flows to find what their value would be currently, finding the net present value. Because money in the present is more valuable than money in the future, the further in the future cash flows are realized, the less valuable they are at present. As a result, the discount factor decreases as the number of years in the equation increases.

Below is a graph showing the declining value of the discount factor over time, with a discount rate of 5%.

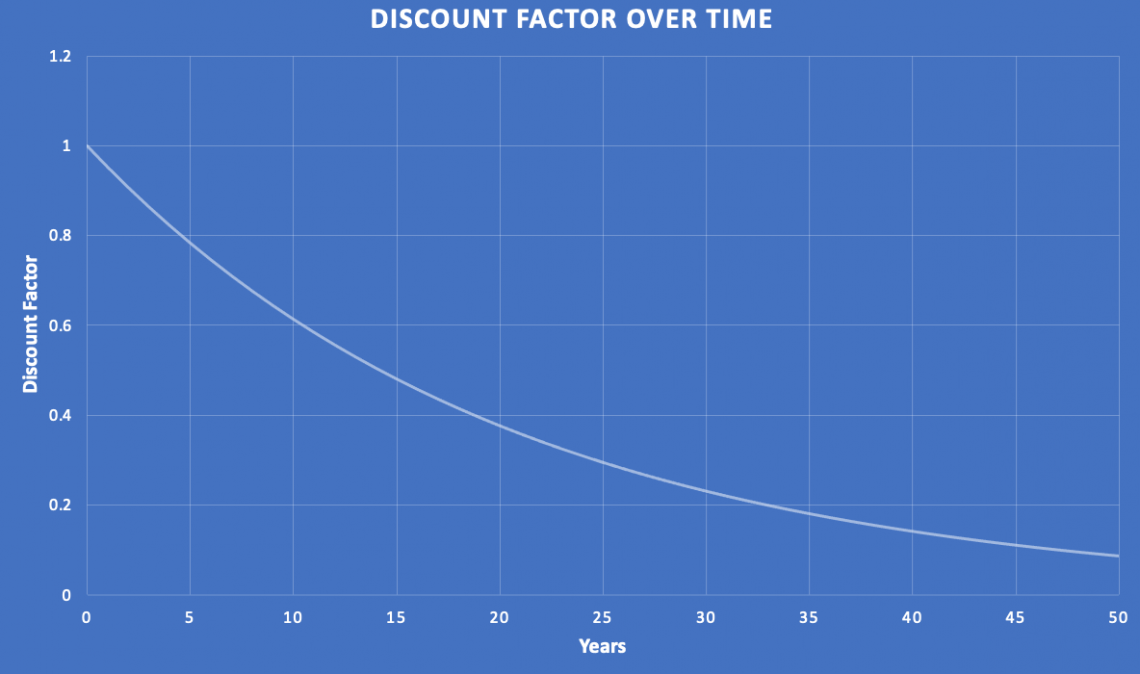
At time 0, it is 1 because time has not decreased the value of the cash flows, and after 50 years, the same sum of money is only worth about 8.7% of its current value at a discount rate of 5%.

Imagine, for example, an investment that costs a company $800. Assuming a discount rate of 5% and the cash flows provided in the picture below in each year, one can use the discount factor to find the present value of all future cash flows.

Subtracting the initial investment from the sum of these values yields the investment's net present value. In this case, the net present value exceeds the initial investment cost, meaning that the investment is profitable and should be pursued.

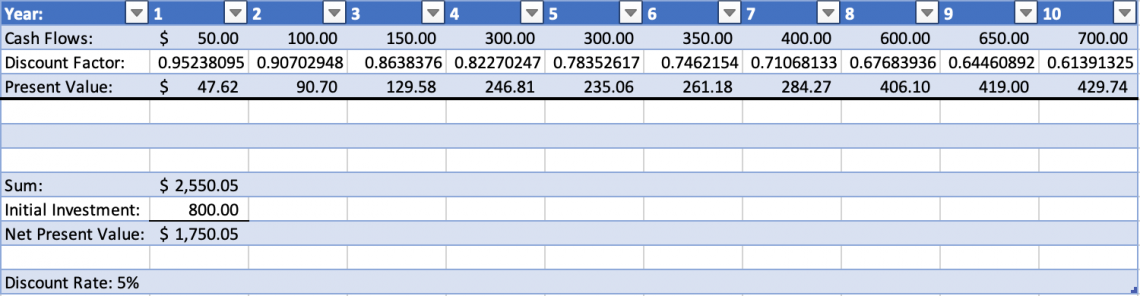
Using the discount factor makes it easy to see exactly how much the cash flows are worth when they are realized. As one can see, the cash flows are the same in years four and five; however, the present value of the cash flows in year five is less than that of year four because more time has passed. Excel also has a built-in NPV function that allows users to find the NPV without finding the discount factor directly. Despite this, it can still be helpful to understand the numbers and double-check one’s work.

More about financial modeling

To continue learning and advancing your career, check out these additional helpful WSO resources:

• What is Financial Modeling?
• Free Financial Modeling Guide
• What Makes a Good Financial Model?
• Top Financial Modeling Courses
• Valuation Modeling in Excel