Internal Rate of Return (IRR)

The internal rate of return is a special discount rate (a rate of return) at which an investment's net present value equals 0. IRR is used in finance, specifically in capital budgeting, as it is one of the most well-known methods of evaluating the profitability of an investment.

A project's IRR is the required rate of return that results in an NPV equal to 0. As a rule of thumb, the higher this rate is, the more attractive the investment will become. This is because it indicates that a project yields higher returns.

This method is called the internal rate of return because it strictly focuses on the return of an investment based on its cash flows. It excludes external factors like inflation, risk-free return rate, capital cost, and financial risk.

Calculating it is very similar to calculating the net present value of an investment. It requires the same formula. The difference is that, in calculating this rate, we are setting NPV equal to zero. 

Net present value is based on the time value of money, the idea that a dollar today is worth more than a dollar due to factors like inflation, opportunity cost, etc. To arrive at NPV, all future cash flows are reduced in value at a "discount rate" to arrive at the "present value" of the investment. 

Note that the rate is a percentage. It is not expressed in dollar terms because it shows the growth rate of an investment or a project. Given an investment's expected future cash flows and the initial cost, we can find the annualized return for that investment.

As a simple example, suppose a $1,000 investment today results in a $1,100 cash flow in one year. This investment's IRR is simply the return on the initial $1,000. Therefore, the internal rate of return for this investment is 10%.

Overview of net present value (NPV)

A business usually decides to invest if it creates more value than it initially costs. An investment creates value when its market value exceeds the cost of acquiring the project. Deciding the market value, however, requires precise estimation methods.

For example, say you bought an empty van for $10,000. Since you are a great interior designer, you furnished the van's inside neatly for $8,000. In addition, you installed the necessary furniture and all living accommodations required for someone to live inside the van.

The van was bought for $10,000, and the total renovations cost $8,000. Therefore, the total initial investment amounts to $18,000. However, being an expert salesperson, you could sell the van for $25,000, $7,000 more than your initial investment.

The market value of the van ($25,000) exceeds its cost ($18,000) by $7,000. That difference is the value created from good management: buying the van, getting materials to furnish it, and making it livable. This management has created $7,000 in value.

This is, of course, a great investment for you to make. However, the difficult part is estimating that the renovated van would sell for $25,000. Every business and company tries to estimate whether an investment is worth making based on the estimated value it creates.

The net profit from this investment is the difference between the market value of an investment and the cost of acquiring it. In our previous case, net profit is positive since the market value of the investment exceeds its cost by $7,000. 

What if we can't observe the market value of the investment? What if the profits will only come far in the future? How do we account for the time value of money?

We will try to use indirect market information, like the estimated cash inflows of the investment, to estimate the NPV of a project. Hence, calculating NPV requires a method called discounted cash flow valuation.

Calculating the net present value

Calculating the NPV of an investment with multiple future cash flows begins with calculating the present value of those cash flows. After calculating the present value of the cash flows, we compare it to the initial cost of the investment:

• If the PV of the cash flows exceeds the initial cost, then we have a positive NPV, so we should take the investment,
• If the PV of the cash flows is less than the initial cost, then we have a negative NPV, so we shouldn't take the investment.
• If the PV of the cash flows is equal to the initial cost, then NPV is equal to 0, so we are indifferent to investing or not.

Suppose a woodworking company is considering investing in a project. The owner is unsure of the future market value that the project will have. However, they can accurately estimate the cash inflows the investment will bring in:

1. At the end of the first year, the project will bring a cash revenue of $10,000
2. At the end of the second year, the project will return a cash revenue of $8,000
3. At the end of the third year, the project will bring a cash revenue of $12,000
4. The project costs $23,000 to launch.
5. The company uses a discount rate of 8%

To calculate the NPV of this project, we first need to calculate the present value of the future cash flows:

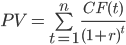
• CF(t) is the cash flow that the investment gives at year t.
• r is the discount rate.
• n is the number of periods between the present and t.

Although this formula seems intimidating, it is simply getting the present value of each cash flow separately. Then, it adds all three present values to get the total present value of the investment to see whether the project is creating value. Therefore,

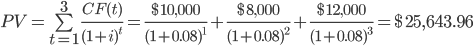
We now know that, at year 0, the project has a market value of $25,643.96. Moreover, the project initially cost the company $23,000. With these numbers, the investment is worth it because it creates more value than the firm originally dedicated to it.

This means that the net present value of the project is positive. However, we should subtract the project's initial cost from its present value to get a more precise measurement. Doing so results in a net present value equal to $2,643.96. 

Since it is a positive number, the company should accept the project and invest. This is the main rule of thumb for a positive NPV. If the NPV were negative, the company would have rejected the project and not invested.

Understanding the internal rate of return 

The IRR method of evaluating an investment or a project is very similar to the NPV method. However, instead of having a certain discount rate for calculating the NPV, we now have to find the discount rate that makes the NPV equal to 0.

Since this metric represents the annualized return of an investment, the higher the rate of return of a project, the more attractive it will be to managers to launch the project. This method is used for investments in various fields, including private equity and venture capital.

For one-period investments, the calculation is fairly easy (see the example at the beginning of the article). However, the measures become more complicated when the investment has multiple cash flows, like in the last criterion.

Suppose there is a $10,000 investment that provides the following cash flows:

1. At the end of the first year, the project will bring a cash revenue of $4,000,
2. At the end of the second year, the project will bring a cash revenue of $3,500, 
3. At the end of the third year, the project will bring a cash revenue of $5,000.

Since multiple cash flows span over three years, the only way to calculate is by setting NPV to zero. That is, we set the NPV of the project equal to zero and isolate IRR in the formula, as we know all other variables.

formula

The formula for calculating RR is the same as the formula for calculating the NPV; the only difference is that we replace NPV with 0 and solve for the discount rate:

If we want to calculate by hand, there is no other choice than to find the internal rate of return through trial and error. That is to say, pick an arbitrary discount rate and work our way to find the desired rate that gives a net present value of 0.

1. Replacing it in the equation for a discount rate of 15% gives an NPV = -$587.66.

This specific discount rate resulted in a negative NPV, so we must choose a lower discount rate.

2. Replacing it in the equation for a discount rate of 10% gives an NPV = $285.50.

This specific discount rate resulted in a positive NPV, so we know that the rate is between 10% and 15% (0.10 < IRR < 0.15). Therefore, we must now choose a discount rate between the two previous rates. So let's go in between.

3. For a discount rate of 12.5%, replacing it in the equation gives an NPV = -$167.35

Since NPV is also negative, we must now choose a lower discount rate to calculate NPV. We carry on this process until NPV becomes as close to 0 as possible. But, of course, it's not possible to have NPV equal to 0 without external assistance, like a financial calculator or a formula.

4. For a discount rate of 11.55%, NPV = $0.72, which is close enough to 0 that we can conclude that IRR = 11.55%

Note that this method is the least efficient way of calculating the internal rate of return. There are other more effective ways, such as using a financial calculator. One of the most common methods is using Excel's IRR/XIRR function.

Advantages

It is one of the most reliable methods of evaluating an investment besides the NPV method. Finding the internal rate of return has a lot of merits, making it more practical in certain situations than simply finding NPV.

1. When discussing and evaluating investments, a firm always prefers to speak in percentages rather than dollars. That is to say; it is always preferred to state the return on investment at an annual rate rather than in dollar terms.

It fulfills this need, while the net present value method does not. Using the internal rate of return provides a clearer way of communicating an investment's profitability than the project's net present value.

For example, here are two ways of conveying the same idea for the same investment. The first is that "undertaking the investment yields a 15% return," while the second is that "using a discount rate of 8%, this investment creates an NPV of $2,000."

For example, which of the two statements more clearly communicates return in a business meeting? For most people, the first statement is better. This is because the first method uses this method as the main indicator of the profitability of a project.

2. Another advantage is that using tNPV requires deciding upon a discount rate. It is not always feasible to find the required return on investment.

However, given the future cash flows of a project, it is quite straightforward to calculate a project's internal rate of return. Therefore, even if the discount rate is unknown, a firm can decide whether to launch a project based only on the rate of return.

For example, the discount rate of a certain investment is unknown because it is the first time such an investment is being undertaken. However, the IRR was calculated to be 35%. This percentage is large enough for a project to accept.

Therefore, in this case, the method was enough to make decisions concerning an investment without having a certain discount rate in mind. Such a high internal return rate should excite the manager to launch the project.

Drawbacks

Despite its numerous advantages, this method may not be useful in certain cases. In those cases, using the net present value method is more practical and reliable in evaluating and making investment decisions.

1. The problem of multiple rates of return

While using this method to decide whether to invest, multiple discount rates can result in an NPV equal to 0.

Specifically, this occurs when a project has non-conventional cash flows. This means the cash flow changes from positive to negative throughout the investment. 

Almost all investments start with a cash outflow, followed by cash inflows. However, there can be projects with cash inflows followed by cash outflows. This mainly occurs because of maintenance or renovation costs.

With unconventional cash flows, calculating the rate will become more complicated, as we usually end up with more than one answer. Neither answer is wrong nor correct. The method can confuse, so using the NPV method is better.

2. Mutually exclusive investment decisions

Suppose a corporation has to choose between two investments, and opting for one investment automatically rules out taking the other. In that case, this represents two mutually exclusive investment decisions.

Assuming that both investments have conventional cash flows, this means that each of them has its internal rate of return. The corporation's task at this point is to choose between two projects rather than decide to take on a single investment.

Intuitively, one can suggest taking on the project with the highest internal rate of return. After all, this metric shows the annualized return of the project. However, while this idea seems plausible initially, we can't use this method to compare two investments.

The project's net present value with the lower rate of return can be higher than that with the higher return. Calculating NPV depends on the required rate of return. For different required rates of return, one project can seem more profitable than the other.

Therefore, with mutually exclusive projects, we should avoid evaluating which one is better based on its rate of return. Instead, to avoid misleading, we must always compare the net present values of the two projects and pick the one with the higher NPV.

Researched and Authored by Vatche Tchelderian | LinkedIn

Reviewed and edited by James Fazeli-Sinaki | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Alpha
• Black Swan Event
• Dodd-Frank Act
• Euro Interbank Offered Rate (Euribor)
• Infinite Banking