Growth Accounting Equation

What is the Growth Accounting Equation?

Unlike most macroeconomics, which is concerned with what occurs throughout the business cycle, this branch of macroeconomics is concerned with what happens over extended periods.

It focuses on the subject of what affects the economy's long-term growth rate and what policy measures might be used to influence it. It's also linked to a more fundamental question of what makes certain countries wealthy while others are impoverished.

The Growth Accounting Equation is a financial instrument that assesses economic growth, especially how changes in available capital, labor, and technology affect changes in a country's real Gross Domestic Product (GDP).

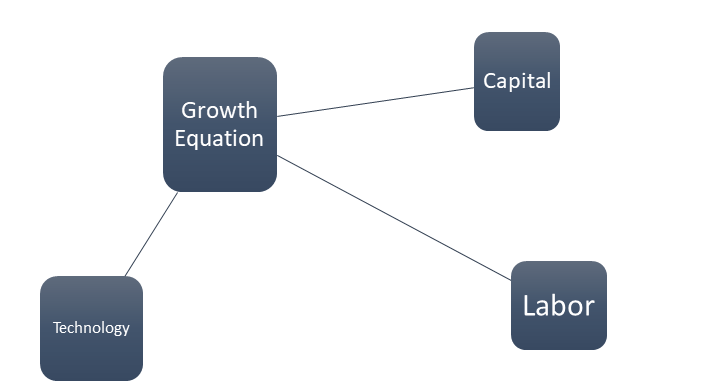
The three key elements are the labor market, capital, and technology leading to a detailed examination of economic growth. 

It breaks down the micro-level economic development into multiple components, providing a very accurate estimate of a country's economic growth.

This concept was created by Robert Solow and Trevor Swan in 1957. Growth accounting was presented for management accounting in the 1980s. Still, it did not survive as a management tool since the production functions in growth accounting and management accounting are understood and stated differently.

The method has been applied to almost every country in the world and provided results stating that the level of economic growth cannot be explained just by changes in the economy's stock of capital or population and labor force growth rates. 

As a result, technical advancement plays a critical role in a country's economic success or lack thereof.

The Equation is a weighted average of the elements involved in growth rates. Three components are included in Solow's economic growth accounting model

• Labor Market Expansion
• Capital Investment, and
• Technology. 

The significant component derived from statistical data releases is capital investment. To explain the remaining gap, Solow added a third factor: technical advancement.

Formula Of Growth Accounting Equation

The Equation allows for a detailed analysis of economic growth. In addition, it allows for the micro-level breakdown of economic development into multiple components, providing a very accurate estimate of a country's economic growth.

The following is the formula to calculate:

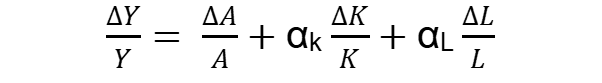
Where, 

• Y is GDP
• ΔY is the change in GDP
• A is the Total Factor of Productivity or Technological advancements
• ΔA is the change in Total Factor Productivity or Technological advancements
• K is the existing capital stock
• ΔK is the change in the capital stock
• L is the size of the labor force
• ΔL is the change in the size of the labor force
• αK is the capital's share of the total income
• αL is labor's share of total income

Growth rates can be positive or negative in this case. As a result, the Equation may be used to assess both a decrease and a rise in real GDP. 

However, the only flaw of the calculation is the difficulty of measuring the pace of technological advancement. As a result, its computation is usually left to the accountant's discretion.

The capital-to-labor ratio is represented by the component "K/L" in the equation. The capital-to-labor ratio measures the amount of total money available per labor unit. The ratio measures the degree to which an economy is capital-intensive.

It indicates whether the economy is capital-intensive. Developed nations, or those with strong economic growth, are more capital-intensive, whereas poorer or emerging countries are more labor-intensive.

The capital-to-labor ratio shows that an economy's living level is determined by the availability of capital and technological improvements, not merely by the percentage growth in employment.

Uses Of Growth Accounting Equation

The equation is utilized in the following situations.

Measure The Source Of Growth

Growth accounting is a mathematical method for analyzing how different factors affect economic growth.

The growth rate of production is the sum of the growth rates of capital, labor, and natural resources, each weighted by their share of national income, plus the rate of productivity growth. 

Assume that efficiency increased by 3% per year and that capital, land, and labor all increased by 4% per year. Then the overall output would grow at a 7% annual pace.

Countries with a rapid increase in per capita income, such as Japan, have high rates of efficiency growth and capital per worker growth.

Countries with low income per capita growth have low efficiency and capital per worker growth rates. We can track production, capital stock, and labor hour growth.

This close relationship suggests that either the efficiency of capital accumulation must be the primary source of growth or that there must be another factor that influences both efficiency and the capital stock that underpins modern economic growth.

Economists commonly use this accounting to break out a country's economic growth percentage from important causes.

Solow's economic growth accounting model considers three essential aspects to give a simplified picture: labor, capital, and technology.

Estimate The Role Of Technological Development

Development accounting divides observed economic growth into components linked to changes in factor inputs and a residual representing technological advancement and other factors.

It is used to calculate the pace of technological advancement in an economy by indirectly computing the contribution of several components to economic growth.

Calculate The Potential Output

The highest quantity of goods and services an economy can produce at total capacity is known as potential output. Likely, work is frequently referred to as the economy's productive capacity.

The production gap can go either positively or negatively, much like GDP. 

Ways of Increasing Outputs

There will be a large number of inputs in every manufacturing process. All of these inputs, however, may be reduced to three components: labor, land, and money. There are only two methods to raise the production per person in any society.

The first method is to increase the quantity of land or money available concerning the number of workers. Because the land area is fixed mainly with population, incomes in contemporary economies are generally increased by growing inputs through capital accumulation.

The second technique to boost output per person is to optimize the manufacturing process so that the same inputs yield more excellent results. Efficiency or Total Factory Productivity (TFP) gains are these terms. Again, gains in efficiency can come from a variety of places.

Better manufacturing technology is one source of efficiency benefits, while economies of scale are another.

Because of the high fixed research and tooling expenses, the marginal cost of producing a vehicle or an airplane is substantially lower than the average cost. As a result, the larger the economy, the higher the output per unit of input.

Better resource distribution within the economy can also result in efficiency advantages. For example, workers move from low-paying agricultural employment to high-paying industrial ones, or money moves from low-return regions to high-return areas.

Even after accounting for all of these factors, such as technology, scale, and legal or political structures, efficiency variations across economies can be seen. For example, two societies might create very different output volumes with the same capital, labor, and land.

Using the Growth Accounting Formulas

Here are some easy growth accounting calculation examples. Try solving the equations independently if you want to understand them better.

Example 1

Assume that a = 0.4, b = 0.6, and c = 0.3, and that employment growth (gL) = 1%, capital growth (gK) = 3%, land growth (gT) = 1%, and technology growth (gA) = 3% in an economy.

(a) What is the capital per worker and land per worker growth rate?

(b) What is the production per worker growth rate?

Solution:

(a) 

Growth rate of capital per worker is gK – gL = 3% – 1% = 2% 

Growth rate of land per worker is gT – gL = 1% – 1% = 0% 

(b)

The growth rate of output per worker is, 

gQ – gL = a(gK – gL) + c(gT – gL) + gA 

= 0.3 x (2%) + 0.3 x (0%) + 3% = 3.6%

Example 2

Assume that gQ = 4%, gK = 2%, gL = 1%, gT = 1.5%, and that a = 1/3, b = 1/3, and c = 1/3.

(a) How fast is production per worker, capital per worker, and land per worker growing?

(b) What is the rate of technological advancement, gA?

Solution:

(a)

gQ – gL = 4% – 1% = 3% 

gK – gL = 2% – 1% = 1% 

gT – gL = 1% – 1% = 0% 

(b)

gA = gQ – a.gK – b.gL – c.gT

= 4% – (1/3).2% – (1/3).1% – (1/3).1.5% = 2.6%

Example 3

Assume that production, capital, labor, and land expand simultaneously. What is the rate of 

(a) production per worker growth? 

(b) technological advancements?

Solution:

(a) 0%, 

(b) 0%  

Example 4

Assume that gQ = 5%, gL = 4%, gK = 8%, gT = 0%, and a = 0.5 and b = 0.3.

What is the:

• (a) rate of increase in production per worker, and 
• (b) rate of increase in efficiency?

Solution:

(a) 

gQ – gL = 5% – 2% = 3%

(b) 

gA = gQ – a.gK – b.gL – c.gT 

= 5 - 0.5(8) - 0.3(4) - 1(0) = - 0.2%

Researched and authored by Ankit Sinha | LinkedIn

Reviewed and edited by Abdul Aziz Rasheedy | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Econometrics
• Economic Calendar
• EDLP
• Fiat Money
• Macroeconomics