Arbitrage
Taking advantage of the differences in price of an asset
What Is Arbitrage?
Arbitrage is the act of simultaneously buying and selling the same or similar asset across multiple markets to generate profit that is often considered risk-free.
It capitalizes on the variation in prices of an asset arising from volatility across both long or short periods of time. Even the slightest difference in price could potentially provide an arbitrage opportunity.
Arbitrage often arises due to market inefficiencies. This market inefficiency could appear anywhere, from the commodities exchange to the farmers’ market.
Many financial theories utilize the concept of no-arbitrage, where some examples include the interest rate parity or the put-call parity.
However, although arbitrage opportunities may sometimes arise, the market could be inefficiently efficient where the cost arising from frictions outweighs the profits generated from this.
Friction (amongst other factors) is probably one of the biggest reasons we sometimes see identical items priced inconsistently in different markets (more on this below).
Proprietary traders are always monitoring markets to exploit these opportunities, whether in derivatives, commodities, or FX. In this day and age, many traders have already developed complex algorithms where machines can detect and capitalize on small price differences through high-frequency trades.
They have always been argued to make the most money, even compared to those in IBD. To get an understanding of the compensation within certain divisions, click here.
Key Takeaways
- Involves simultaneous buying and selling of assets in different markets.
- Interest rate parity demonstrates complex arbitrage with interest and exchange rates.
- Capitalizes on inconsistent exchange rates among multiple currencies.
- Theoretical risk-free strategy may fail due to transaction costs.
- Dual-listed company case studies reveal volatility and uncertainty.
Examples of Arbitrage opportunities
The simplest example arises when you go to store A and see bananas selling for $1, while at store B, it sells for $2. You would generate arbitrage by buying bananas from store A while selling them at store B.
The table below illustrates this example better:
| Units | Price | Profit (Loss) | |
|---|---|---|---|
| Buy bananas from Store A | 250 | $1 | ($250) |
| Sell bananas to store B | 250 | $2 | $500 |
| Outcome |
$250 |
||
You just made $250 buying and selling the same item by exploiting the price difference across different markets.
Congratulations! The number of units here was 250, but this is an arbitrary number. In practice, you should buy as many as possible to enjoy maximum profits while also making the WSO army of monkeys proud.
You might be wondering, what is the outcome of your banana arbitrage generating strategy?
As you are buying a significant amount of bananas from store A while selling them at store B, you increase the demand in store A while flooding the supply in store B.
As the law of supply and demand stipulates, prices increase with higher demand and go down with increasing supply. Therefore, your actions would push the prices of bananas in store A up while simultaneously decreasing the prices of bananas in store B.
An outcome is that the market for bananas stabilizes (somewhere between $1 and $2) and becomes more efficient as prices are now consistent across markets.
Interest rate parity: Exchange rate and Interest Rate
Here is a more complicated but realistic example of profiting from the different interest rates and exchange rates.
Consider a world where the risk-free rate in the United States is 5%, whereas the risk-free rate in the United Kingdom is 1%.
The current UK/US spot rate is £0.73 per US dollar. There are currently forward contracts where the 1-year forward exchange rate for the US dollar is £0.725 per US dollar. This presents an opportunity for free money.
For example, you could borrow at the UK risk-free rate and convert at the current spot rate to save money at the US risk-free rate. Then, at the end of one year, you could exchange the money back at the aforementioned forward rate and repay your loan.
Here’s how it would work:
- Enter into a forward contract and agree to convert $10,500 at the current forward rate of £0.725 per US dollar.
- Borrow £7,300 with 1% interest from the UK bank
- Exchange the £7,300 at the current spot rate to receive $10,000
- Save $10,000 at the risk-free rate of 5% with the US bank
- At the end of the year, receive $10,500
- Convert $10,500 back into pounds at the £0.725 per US dollar rate, receive £7,612.50
- Repay your loan with interest at £7,373.
- The remaining money of £239.5 (£7,612.5 - £7,373) is yours to keep!
This opportunity was present because of multiple factors.
- Firstly, the interest rates were different across both countries - it was more attractive to save in the US rather than in the UK. Hence, it would make sense for people (including foreigners) to prefer saving money in the US.
- While the forward rate did show that the Pounds would appreciate, the rate at which the Pounds appreciated was still lower than the difference in interest rates. The forward rate predicted a roughly 0.68% appreciation in the Pounds. However, the difference in the interest rates was 4%.
- As long as the forward rate is not equal to the difference in interest rates, this arbitrage opportunity will always exist. In fact, the wider the difference, the more inefficient the market is, and the greater the profits are from this strategy!
Triangular arbitrage: multiple currencies
In the forex market, the exchange rate for currencies is always changing. Sometimes, the exchange rates are not always consistent amongst multiple currencies due to volatility. This provides FX traders the opportunity to engage in triangular arbitrage.
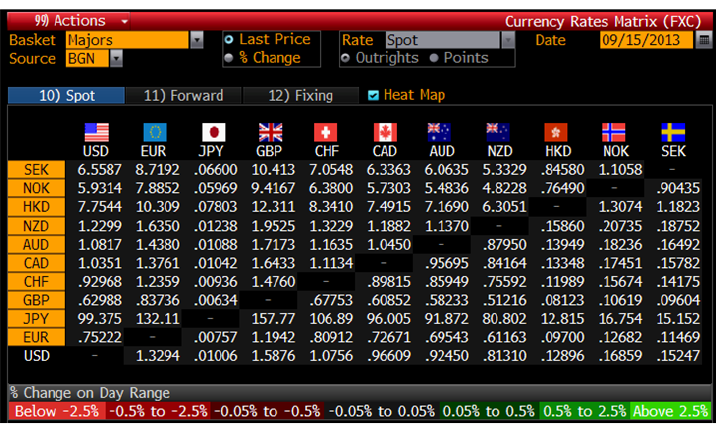
Suppose that at one instantaneous point in time the following exchange rate for 3 currencies are as follows:
- EUR/GBP = 1.19047
- EUR/USD = 0.87719
- USD/GBP = 1.36366
Let’s see what happens when you multiply the EUR/USD and USD/GBP exchange rates.

We find that it’s different from the listed EUR/GBP exchange rate at 1.19047!
Here is what you could do to profit from this scenario:
- Sell £100,000 for $136,366 at USD/GBP= 1.36366
- Exchange $136,366 for €119,618.90 at EUR/USD= 0.87719
- Exchange €119,618.90 for £100,480.40 at EUR/GBP= 1.19047
- £100,480.40 - £100,000 = £480.40
- You just made £480.40 instantaneously. Woo hoo!
How do you identify this? First, compare the listed EUR/GBP exchange rate versus the one you derived by trading USD in between.
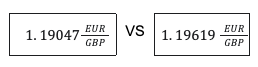
Therefore, you sell GBP using the more expensive exchange rate and buy GBP using the less expensive exchange rate. Free money!
When has Arbitrage failed?
Theoretically speaking, this strategy does seem like riskless free money when you crunch the numbers. But unfortunately, this doesn’t always work in practice.
When you purchased and sold those bananas between stores A & B, there was no factor of your effort. There were no transaction costs involved when you bought those forward contracts or exchanged money in the forex market.
In the triangular example above, you put up £100k just for £480, and in most cases, that £480 would not exist once transaction fees are counted.
In fact, you’d probably lose money given the number of transactions you had to make to generate that profit.
One of the biggest hedge fund failures in history was the collapse of Long-Term Capital Management (LTCM).
The fund was founded by Salomon Brothers trader John Meriwether in 1994 and had two principal shareholders: Myron Scholes and Robert Merton (creators of the Black Scholes option pricing formula and Nobel Prize Winners).
The fund started with $1.25 billion in capital and was extremely successful initially, boasting an after-fees annual return of 35% for the first 3 years. By 1996, the firm had an AUM of over $140 billion and had more than 100 workers.
LTCM’s strategy mainly revolved around deploying arbitrage strategies within Fixed Income. However, in later years, the fund applied these strategies to Equity.
One of LTCM’s bets in 1998 included exploiting the spread between dual-listed stocks, namely Royal Dutch Petroleum Co., listed on the Amsterdam Stock Exchange, and Shell Transport & Trading Co., listed in London.
At the time, these two companies entered an agreement to combine their interest on a 60/40 basis while remaining as separate entities. Because of this, the companies share the same profits and should trade in the same direction at the same percentages.
LTCM noticed that these companies were not trading synonymously, and there was a significant spread between the two. The idea? Short the expensive stock (in this case, Amsterdam’s Royal Dutch) and long the underpriced stock (London’s Shell Transport & Trading).
As long as these stocks converged into parity, the gains from either trade would cover the loss from the other. Unfortunately, due to certain economic events that transpired, both stocks diverged further rather than converged (which was expected).
As a result, LTCM had to cover its Royal Dutch short and sell its Shell position at a wider spread than when they entered the trade, resulting in heavy losses. As a result, the hedge fund eventually collapsed in the early 2000s.
Source: Business Insider | WSJ
One paper published by Erasmus University in 2008 studied 12 dual-listed companies and found that all of them diverged from parity (they did not trade at the same prices).
While they did conclude an abnormal annual return of roughly 10% when deploying arbitrage strategies, there was significant volatility and no predetermined date at which prices would converge.
Basically, suppose you had deployed arbitrage strategies for these 12 dual-listed companies. In that case, you’d be dealing with a fair amount of uncertainty, and you’d have to diamond hands the losses and wait until prices converged.
Unfortunately, the time horizon for you to realize profits maybe years, and with LTCM, they went bust before prices could stabilize.
Everything You Need To Master Valuation Modeling
To Help You Thrive in the Most Prestigious Jobs on Wall Street.
Researched and authored by Jasper Lim | Linkedin
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:



or Want to Sign up with your social account?