Call Option
A derivative instrument that allows the holder the right, but not the obligation, to buy an asset from the writer of the option at a predetermined strike price within or on the expiration date, depending on the nature of the option bought.
What Is A Call Option?
A Call Option (commonly referred to as a Call) is a derivative instrument that allows the holder the right, but not the obligation, to buy an asset from the writer of the option at a predetermined strike price within or on the expiration date, depending on the nature of the option bought.
There are two primary types of calls, i.e., the American and European calls. Each has different rules around what rights are given to the holder.
- American Calls: The holder is allowed to exercise the option as long as it is within the expiration date.
- European Calls: The holder can only exercise the option on the expiration date. This is the most common type of option among the two.
In practice, this makes a big difference as the American type is more flexible than its European counterpart and, therefore, commands a premium over the latter’s price (other things being equal).
Below is a graph illustrating the relationship between the payoff on a call and the underlying stock’s price.
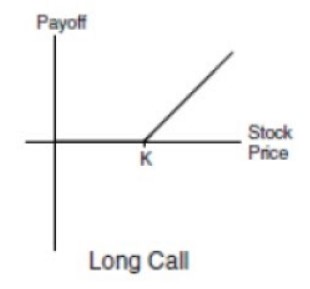
Key Takeaways
- A call option gives the holder the right, but not the obligation, to buy an asset at a predetermined price by or on the expiration date, with American and European options being the two primary types.
- In-the-money calls have the asset's price above the strike price, while out-of-the-money calls have the asset's price below the strike price, affecting their intrinsic and extrinsic values.
- A covered call strategy involves selling call options on owned assets, providing downside protection while sacrificing some upside potential.
- A straddle strategy involves buying both call and put options with the same strike price and expiration date, used when expecting increased volatility but uncertain about the direction.
- Call options can be priced using models like the Black-Scholes-Merton Model for European options without dividends and the Binomial Option Pricing Model, which generates a price tree to determine option value.
“In-the-money” vs “out-of-the-money” calls
A call would be considered “in-the-money” if the underlying asset’s price is above the predetermined strike price and, therefore, would possess intrinsic value. More simply, this means that if the option holder exercised the right to buy, they would get a payout.
On the other hand, a call with the underlying asset’s price below the predetermined strike price would be considered “out-of-the-money” and only possess extrinsic value.
More simply, this means that if the holder exercised the right to buy, it would be worth nothing right now, but because there is still some time before it expires, it still has some worth (the option could move into the money before it expires).
Examples of factors that contribute to the extrinsic value would be the volatility of the underlying asset (measured by vega) or the time to expiration (measured by theta) of the option (recall Time Value of Money concept).

In-The-Money Example
Let’s say investor A buys a call on Tesla stock at a strike price of $1,000 per share that expires in 6 months. This can be expressed as follows:
- Strike Price: $1,000
- Time to Expiry: 6 months
- Underlying Asset: TSLA
Let’s assume that the price of a Tesla share is above the $1,000 strike price. In this example, let’s assume it trades at $1,100.
Then, we would call this option “in-the-money” because Investor A has the right to buy the share at $1,000 (which can be sold in the open market for a profit of $100, i.e., $1,100 - $1,000).
Out-Of-The-Money Example
Continuing the example above, let’s say investor A buys a call on Tesla stock at the same strike price of $1,000 per share that expires in 6 months. This can be expressed as follows:
- Strike Price: $1,000
- Time to Expiry: 6 months
- Underlying Asset: TSLA
Let’s assume Tesla stock is trading below the $1,000 strike price.
In this example, let’s assume that it is trading at $900, in which case we would call this option “out-of-the-money” because you have the RIGHT to buy something for $1,000 that is only currently worth $900 (pretty worthless right now… but is it?).
So, in a vacuum, the fact that this option is out of the money is not good for Investor A, who holds that right.
Note
Even though this option may be “out-of-the-money”, it doesn’t mean it doesn’t have any value.
Since the option still has time before it expires, there is a possibility it would become “in-the-money” before the expiration of the option. This is especially true for a very volatile stock like Tesla (or any underlying volatile asset).
For a more detailed explanation, check out this video:
Covered calls
A covered call is an options trading strategy in which the investor owns the underlying asset (usually stocks), but they believe that the underlying asset price would have little to no increase in value in the short term.
As part of this strategy, the investor would sell the options on the owned asset to potential buyers and bag the fees (generally called a premium) from underwriting them. After underwriting the options, the following scenarios may take place:
- Asset price below the strike price: The call holder does not exercise the option, which leads to the investor profiting from the option sale, thereby mitigating the loss to a certain degree on the long asset position
- Asset price above strike price: The option holder would exercise the option, and the investor would have to sell the asset at the predetermined strike price. Hence, the investor profits from the sale of the asset while bagging the premium
- When the asset price is equal to the strike price: The holder will not exercise the option, and the investor gains the profit from the underwriting premium as there is little to no gain in the underlying asset
Therefore, a covered call is a risk-mitigating option strategy by obtaining some downside protection while sacrificing upside potential.
Straddle using calls
Another strategy involving the use of calls is a straddle. This involves the simultaneous purchase of a call and a put option with the same strike price and expiration date.
This strategy is typically implemented when an investor is convinced that the option’s underlying asset is prone to increased volatility but has less conviction in which direction the pricing will move.
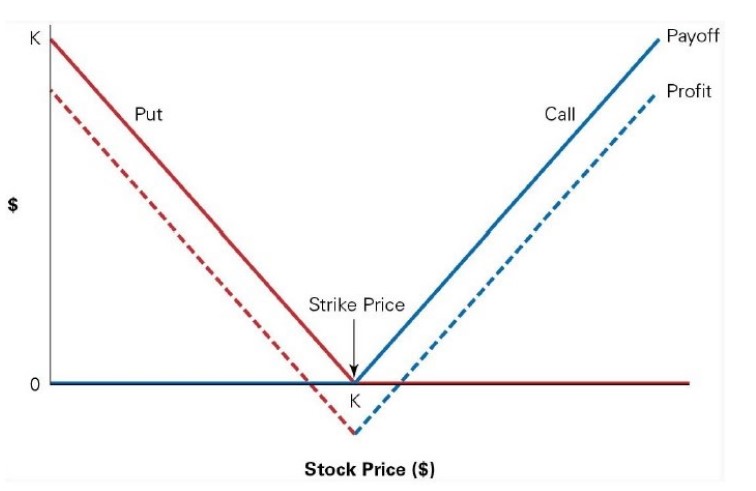
Example of a straddle trade
An example of when a straddle trade might make sense was during the March 2020 stock market crash.
In this case, when investors may take a while to form an educated opinion on the full impact of the COVID-19 crisis, Saudi-Russia oil price war, and the closing of borders by countries, a straddle trade would allow them to bet on volatility-increasing without an opinion on if prices will continue to drop or shoot back up with the announcement of stimulus packages (for example).
Many derivative traders, taking advantage of the high volatility reflected in the VIX index, employ it in their trading when there is no definitive conclusion if the stock markets have “bottomed” or will continue to decline.
Factors Affecting Call Options
In general, five factors affect their value. They are:
1. Strike price
The strike price is the predetermined price at which the option holder can exercise the option to buy the underlying asset from the option seller. The strike price has a direct relationship with the value of a call.
Purchasing an option with a high strike price with the same expiration tends to be cheaper as the intrinsic value of a call reduces with a higher strike price. The image below illustrates the same:
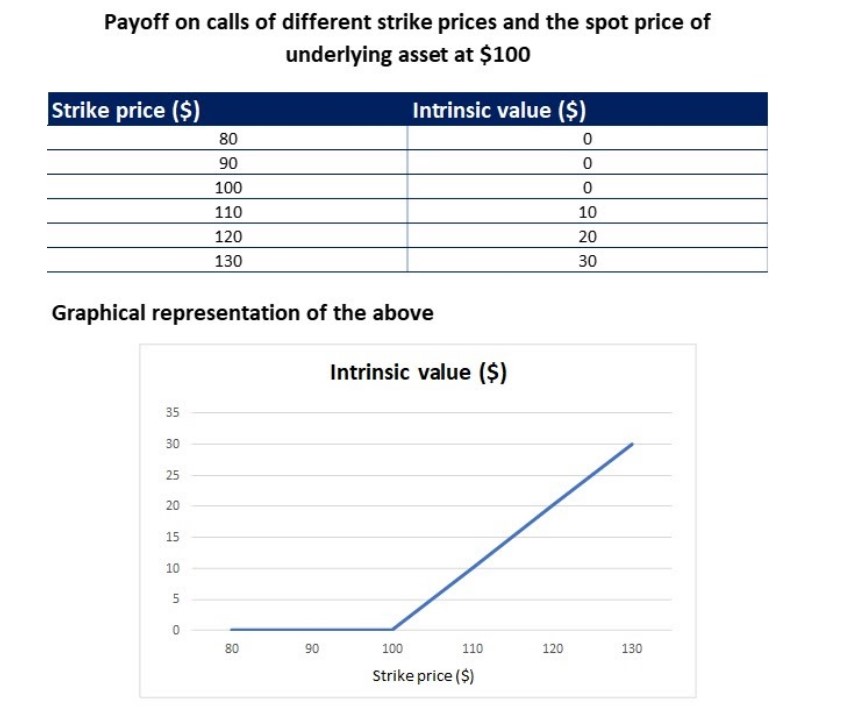
2. Price of the underlying asset
The price of the underlying asset affects the value of the call directly. When there is an increase in the price of the underlying asset, there is an increase in the value of the call, as this means that there is a higher probability that it is “in-the-money”.
This makes it more likely that it would be exercised and hence has intrinsic value, which in turn increases its value. The direct effect of change in the underlying asset’s price on an option’s price is explained through a factor known as delta.
3. Time to expiration
The time to expiration of the call directly affects its value. The longer the expiration time, the higher the option’s value. As the option nears its time to expiration, the value of the call keeps decreasing.
This is due to the effect of the time value of money and is also called the time decay of an option, explained otherwise through a factor called theta.
4. Interest rate environment
The prevailing risk-free interest rate directly affects the value of the call, as when the interest rate is high, there is an increase in its intrinsic value. This is because buying calls, especially when “in the money”, is analogous to buying an underlying asset with credit.
As the holder pays only the option premium today and will pay the exercise price only during their exercise of the option, a high interest rate means that the strike price has to be discounted at a higher rate.
As we recall from the first factor, the lower the strike price, the higher the value of the call. Hence, a high interest rate leads to an increase in the price of the call to adjust for this increased discounting factor.
Note
The effect of interest rate on the option’s value is captured while calculating the effect of the time value of money on the option price or its theta.
5. Implied volatility of the underlying asset
The implied volatility (IV) of the underlying asset affects the value of the call. When the IV of the underlying asset is high, there is an increase in the extrinsic value of the call.
This is because when the IV of the underlying asset is high, there is a possibility for a big increase in value, leading to the said option expiring “in-the-money”. This pushes up its expected value and, therefore, the premium on it.
Further, to explain the concept of IV, it is only possible to estimate the future volatility of an underlying asset with credible information. Therefore, investors would use the historical volatility of the underlying asset to infer the future volatility of the underlying asset.
This is commonly known as implied volatility (IV), and its effect on price is measured using vega.
Pricing a call
There are many ways to price a call. This section will discuss the most common ways to value it, namely the Black-Scholes-Merton Model and the Binomial Option Pricing Model.
1. Black-Scholes option-pricing model
The Black-Scholes-Merton Model (more commonly known as the Black-Scholes Option Pricing Model) won its creators the 1997 Nobel Memorial Prize in Economic Sciences. It is used to value European options that do not pay dividends.
If the underlying asset pays dividends, an adjustment could still be made to fit it into the Black-Scholes model. The adjustment is as follows:
Sx = S - PV(Dividends)
Where:
- Sx = adjusted underlying asset price
- S = underlying asset price
- PV (Dividends) = present value of all dividends to the expiration date of the option
Once the adjustment is made, it can be applied to the Black-Scholes formula to derive the value of the European call. The formula of the Black-Scholes model to derive the value of a call is as follows:
C = (S * N(d1)) - (N(d2) * Ke(-rt))
Where:
- d1= (ln(S / K) + ([r + (s2 / 2)] * t)) / (s* √t)
- d2= d1 - (s * √t)
- C = Value of call
- S = Asset price
- t = time to expiration
- K = Strike Price
- r = risk-free rate
- N = cumulative standard normal distribution
- s = standard deviation
2. Binomial option pricing model (BOPM)
Alternatively, it could also be valued using a Binomial option pricing model (alternatively known as BOPM). The BOPM was first proposed by William Sharpe (more commonly known for his work on the Capital Asset Pricing Model (CAPM) and the Sharpe ratio) in the 1978 edition of Investments (ISBN 013504605X).
It is a lattice-based model where a price tree is generated to derive the option’s value. An example of a price tree is as follows:
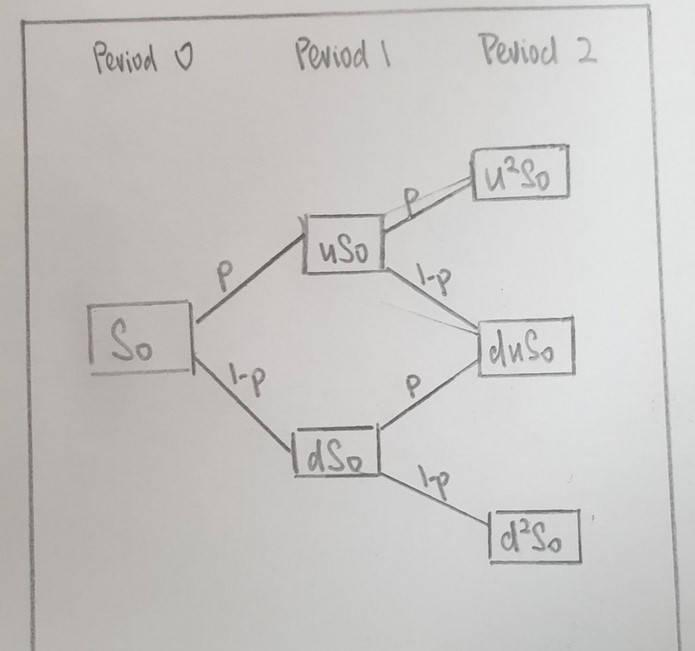
First, the values of the outcomes are derived. They are the intrinsic value of the option at the expiration date and can be defined as:
Max [(Sn - K) , 0] for the call
Where:
- K = strike price of the option
- Sn= price of the underlying asset at the nth period
Next, after discovering all the outcome values, we use a risk-neutral assumption to determine the probability of occurrence of the option’s upside and downside cases.
In this model, the underlying asset’s volatility can be estimated using historical data. The formula for calculating the risk-neutral probability is as follows:
π = (Rf - d) / (u - d)
Where:
- π = probability of upside
- Rf= risk-free rate of a period in % form
- u = upside case of a period in % form
- d = downside case of a period in % form
Then, once the probability of upside is known, we could derive the value of the option at an earlier period by deriving the value of the option at each node working backward, adjusting for the probability, and so on until we eventually reach period 0, which is the current value of the option.
The formula to derive the value of the option at an earlier period is as follows:
π = (probability of upside * Xu) + [(1 - probability of upside) * Xd] / (1 + Rf)
Where:
- π = probability
- Xu= upside case of derivative
- Xd= downside case of derivative
- Rf= risk-free rate during the period
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:



or Want to Sign up with your social account?