Net Present Value (NPV)
Discounting the value of all future cash flows over an investment's entire life to the present
Net present value (NPV) is a method of valuation where the value of an asset or business is considered equal to the sum of the discounted future cash flows it generates. Discounting the future cash flows allows adjusting the risk inherent in an investment. This intrinsic valuation method compares the present value of future cash flows with the initial investment to evaluate profitability.

An appropriate discount rate needs to be calculated to discount the future cash flows. The rate can be a required rate of return, the weighted average cost of capital (WACC), or the risk-free rate. Discounting the future cash flows helps to account for the risk of a particular investment and the time value of money.
The time value of money is a financial concept that assumes money available in the present is more valuable than the same amount of money in the future. This is because money in the present can be invested to generate returns over time.
Net present value differs from the present value in that it accounts for the initial cash outflow involved in an investment. The present value represents the discounted future cash flows. The net present value will represent the discounted future cash flows left over after subtracting the initial investment.
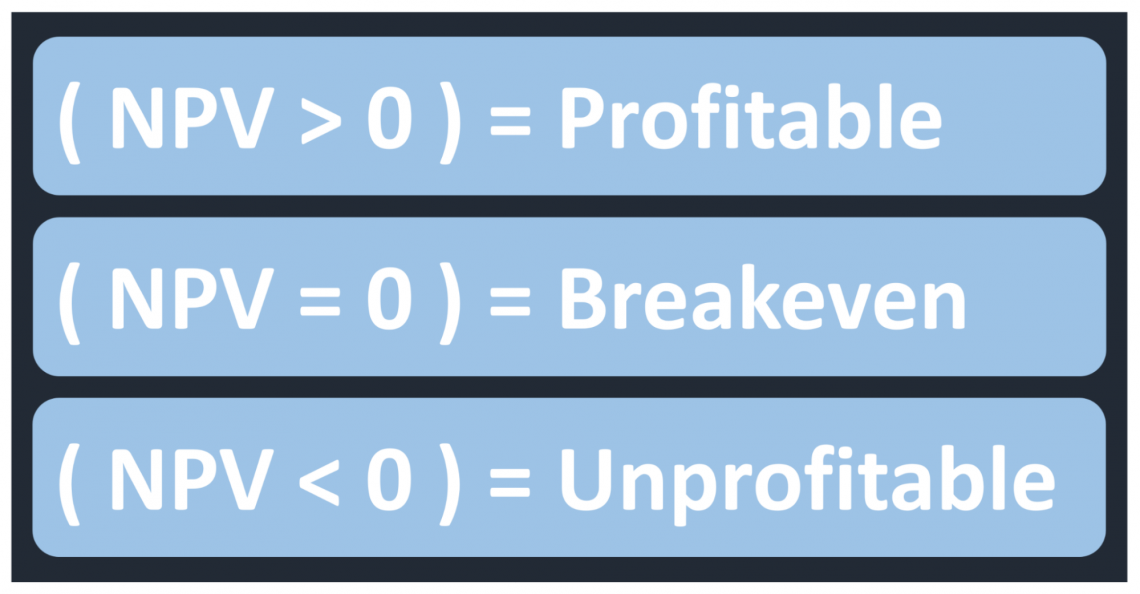
When the net present value is positive, it indicates that the investment opportunity will be profitable. This means that the discounted value of the investments’ future cash flows surpasses the initial capital invested. Therefore, in theory, only investment opportunities with a positive net present value should be undertaken.
Meanwhile, if the net present value is negative, it indicates that the investment opportunity will lose money. This means the discounted value of the investment’s future cash flows is less than the initial capital invested.
If the net present value equals zero, the investment will not be profitable or unprofitable but will break even. This means the discounted value of the investments’ future cash flows equals the initial capital invested.
The Italian mathematician Fibonacci is the first person on record to discuss present value. In his book Liber Abaci published in 1202, he discussed various topics, including the Fibonacci series, international trade, distributing joint venture profits, and present value. Fibonacci illustrates the concept of present value with an example that involves a king issuing an annuity to a soldier.

Economist Irving Fisher modernized the concept of net present value in the early 1900s. Irving Fisher’s book The Rate of Interest, published in 1907, revitalized the use of present value for assessing prospective investments. In the book, he claimed that the true value of an asset was the present value of the asset’s future generated income.

Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:




or Want to Sign up with your social account?