Nash Equilibrium

What is Nash Equilibrium?

The Nash equilibrium is a game theory concept used in non-cooperative games to determine the best strategy for all the players. The equilibrium is present when each player has chosen a strategy and no player has anything to gain by changing their strategy.

In addition, an equilibrium exists when all players are playing the same strategy and no individual player can benefit from switching to a different one.

• This concept is best illustrated with a payoff matrix. The payoff matrix highlights the different outcomes (payoffs) for each player depending on what strategy they choose.
• By analyzing the payoff matrix you can see how results will vary for each player depending on their chosen strategy. 
• Prior to the development of this concept, markets were analyzed through the lens of supply and demand. Economists lacked the ability and knowledge to analyze a given market based on its rules.
• Markets can vary depending on their rules and prior to its development, there was no way to account for their effect on potential outcomes. 

Moreover, prior to the development of this theory,  the dominant economic ideology was based upon Adam Smith’s economic theory of the invisible hand which was introduced in The Theory of Moral Sentiments in 1759 and later perfected in The Wealth of Nations in 1776. 

• The invisible hand theory claimed that individuals pursuing their own self interest would create positive benefits for society.
• The development of Nash equilibrium proved that individuals acting in their own self interest could produce negative outcomes for society, sometimes even on a catastrophic level.
• The theory was developed by John Nash. John Nash was a mathematician and economist who won the nobel prize for economic sciences in 1994.

In 1998 a movie based on his life was produced called A Beautiful Mind. It was directed by Ron Howard and cast Russel Crowe as John Nash.

While the beginning of the movie centers around his economic and mathematical achievements, the majority of the movie centers around Nash’s lifelong struggle with schizophrenia.

Understanding Nash equilibrium

The Nash equilibrium occurs when within a game a set of players have a chosen strategy that they would not want to deviate from based on the strategies of the other participating players.

In this equilibrium every player achieves the best possible outcome considering the strategies that other players in the game have employed. 

However, it does not necessarily mean that every player gets the outcome they most desire. 

Any given game may have:

• One equilibrium
• No equilibrium
• Multiple equilibriums 

The Nash equilibrium takes place within a non cooperating game. A cooperating game often has an external force of authority or some sort of threat that forces cooperation within a group. 

Players in a cooperative game work together towards a common goal for the benefit of the group. 

However, in a non-cooperative game, individuals compete against each other and the main goal of the individual is to acquire a payout that is self beneficial. 

This concept made fundamental contributions to game theory. Game theory is a field of study in which mathematical models are utilized with the intention of understanding how and why people make decisions in everyday life.

Insights discovered in game theory have implications for economics, politics, sociology, and computer science.   

Here is a very basic scenario that highlights the decisions and potential outcomes that occur when two drivers approach an intersection.

The digits within the quadrants represent each driver and their potential payoff based upon what decision they choose to make and what the other driver chooses to do.

• In the top left quadrant we can see that if both drivers do not stop at the intersection they both receive a negative payout of 3 because they would crash into each other. 
• In the top right quadrant we see the payouts for driver #1 stopping at the intersection and driver #2 going through the intersection. Driver #2 receives a payout of 1 because they don't lose any time. Diver #1 receives a payout of 0 because they have to stop and wait for driver #2 to pass, though driver #1 still gets to go after driver #2 avoiding a crash and getting to their destination slightly delayed. 
• In the bottom left quadrant we see the same result as the top right quadrant except with the roles reversed. In this scenario driver #1 goes through the intersection and driver #2 stops and goes after. 
• In the bottom right quadrant we see the scenario where both drivers stop resulting in a payout of negative 1 for both drivers. In this scenario neither of the drivers crash, though both drivers stop and never get to pass through the intersection which is why the payout is negative. 

There are actually two equilibriums within this example. Both occur in the scenarios in which one driver stops and the other driver passes through the intersection. The most optimal strategy for the drivers is to have one driver stop and the other driver go.

There is no incentive for either driver to stop, nor is there an incentive for either driver to drive through the intersection producing a car crash.

Jean Jacques Rousseau hypothesized that the most optimal choice for both hunters would be to work together. This is because hunting the stag would produce the highest payout.

• In the top left quadrant both hunters work together to hunt the stag and acquire 3 pieces of meat for each of them. 
• In the top right quadrant hunter #1 hunts the stag though is unsuccessful because it takes 2 hunters working together to successfully hunt a stag. Hunter #2 hunts the rabbit and is successful in acquiring 2 pieces of meat. 
• The bottom left quadrant produces the same result as the top right quadrant though with the roles reversed. Hunter #2 hunts the stag and is unsuccessful while hunter #1 hunts the rabbit and acquires 2 pieces of meat. 
• In the bottom right quadrant both hunters choose to work separately and hunt the rabbit. This results in both hunters receiving 1 piece of meat each.

The stag hunt produces multiple equilibriums. The equilibriums occur when either both hunters choose to work together to hunt the stag or when both hunters choose not to work together and individually hunt the rabbits. 

This particular scenario brings about a philosophical argument. It is the most optimal for both hunters to work together because it produces the highest payout. Hunting together produces 3 pieces of meat for each hunter opposed to hunting alone which produces 1 piece of meat for each hunter.

But will the hunters choose to work together? The stag hunt highlights how important trust can be between multiple parties within the decision-making process:

• If the hunters are able to trust each other then they can work together to acquire more meat.
• If the hunters cannot trust each other then they have to hunt alone and end up acquiring less meat. 

This philosophical realization has profound impacts for the world both economically and socially. Theoretically, you could have a scenario where 2 or more parties do not choose the most optimal outcome for themselves because the parties lack trust. 

David Hume was a Scottish philosopher in the 1700s who understood the implications of this theory. 

He created two scenarios that highlight how trust and cooperation can result in positive economic and social impacts:

1. The first scenario involves two men in a boat together. If they both row the boat together then they are able to move, though if one of them or none of them row the boat then the boat will not move. 
2. The second scenario involves two men draining a field. If they both work together to drain the field then they will be successful. If one of them drains the field or if neither of them drain the field then the field will not be successfully drained.

the Prisoner's Dilemma in the Context of Nash Equilibrium

The prisoner's dilemma was originally created by Merril Flood and Melvin Dresher in 1950. It was later reworked by Albert W. Tucker by adding prison sentences to act as negative payouts. Albert W. Tucker officially named the game the prisoner's dilemma. 

The point of the game was to highlight why two parties may choose not to cooperate despite cooperation being the most optimal strategy for both parties. 

In the prisoner's dilemma, two people are arrested and placed in solitary confinement. Communication between individuals is not allowed. The prosecutors offer each individual the opportunity to confess that the other is the one who committed the crime.

A variety of negative and positive payouts are offered to the players affecting which strategy each player will choose to adopt. 

• In the top left quadrant we see the scenario for both players remaining silent. If they both stay silent they will each serve 1 year in prison. 
• In the top right quadrant a scenario in which prisoner #2 chooses to confess that prisoner #1 committed the crime. Prisoner #2 goes free and prisoner #1 serves 8 years in prison
• In the bottom left quadrant we see the same scenario as the top right quadrant but with the roles reversed. In this scenario, prisoner #1 confesses that prisoner #2 is the one who committed the crime. Prisoner #1 goes free and prisoner #2 serves 8 years in prison.
• In the bottom right quadrant we have a scenario in which both players confess. This results in both prisoner #1 and prisoner #2 serving 5 years in prison. 

In this example, Nash equilibrium occurs in the bottom right quadrant in which both players choose to confess and end up serving 5 years in prison, and in the top left quadrant in which both players choose to stay silent and serve 1 year in prison. 

Despite the most optimal outcome for both players being to cooperate and stay silent to only serve 1 year in prison, both players lack trust in their counterparts to stay silent.

In addition, both players are incentivized to confess by having the potential opportunity to go free and not serve any time in prison. 

This example does a good job of highlighting how people may sacrifice the most optimal payout for both themselves and the group due to a lack of trust and an inability to cooperate. 

Insights and Implications from Nash Equilibrium in Game Theory 

The Nash equilibrium highlights how choices are made by individuals within a game. What we find is that individuals pursue their self-interest while taking into account the strategies of other players within the game. 

When we apply this realization to human society, we see that individuals who pursue their self-interest end up sacrificing the most optimal outcome for everyone as a whole. 

Depending on the situation, the most optimal outcome may be for the individual alone, society as a whole, or for both the individual and society simultaneously. It is possible for a selected strategy to end up with a suboptimal payout for both the individual and the community. 

Before the Nash equilibrium, it was believed that each individual who pursued actions in the pursuit of self-interest would produce net positives for both themselves and the world. Post Nash equilibrium we have found that it is far more complicated.

This theory has profound implications for the economic understanding of social organization in the present day. 

If we take climate change as an example, we can see that countries may be incentivized to ignore carbon emissions for the sake of increasing economic output, i.e., pursuing their self-interest.

This strategy creates a short-term self-serving benefit, for the risk of a potentially long-term negative payout due to the increasing effects of climate change. 

It is important to remember that payouts affect decision-making. The more intense the payout whether negative or positive, the more effect it will have on an individual's selection of a given strategy.

Trust and cooperation are social factors that can alter the results of an individual's selected strategy. If two parties can trust each other and cooperate, they may pursue their self-interest together and potentially receive a higher payout, as opposed to working alone. 

Successful forms of this concept in everyday life include any group that forms together in order to accomplish a common goal, think companies, sports teams, and governments. 

To learn more about the role that trust and cooperation play in-game theory take a look at this online game.

Examples of Nash Equilibrium

This equilibrium occurs when each player in the game is making the best decision that they can, taking into account the decisions of the others.

Understanding this equilibrium is essential for fields ranging from economics to political science. But, as with many theoretical concepts, real-world examples can help clarify and illuminate its intricacies

How does this abstract concept play out in real-world scenarios?

Baseball and Steroids

In baseball, the game would be best played if no player were to use performance-enhancing drugs. An issue that arises in a scenario in which all players within a game are following the rules, is that it creates an incentive for any given individual to use drugs in order to get a leg up on the competition. 

If one player decides to use performance-enhancing drugs it then incentivizes all players to use them in order to have the game become fair again. 

In 2001, Barry Bonds, a player for the San Francisco Giants, set the single season home run record with 73. In 2007, he surpassed Hank Aaron for the most home runs of all time with 756. 

Within the baseball world it is widely accepted that Barry Bonds used steroids in order to enhance his level of play. While he has the most home runs of all time he still hasn't been inducted into the hall of fame because of his steroid use.

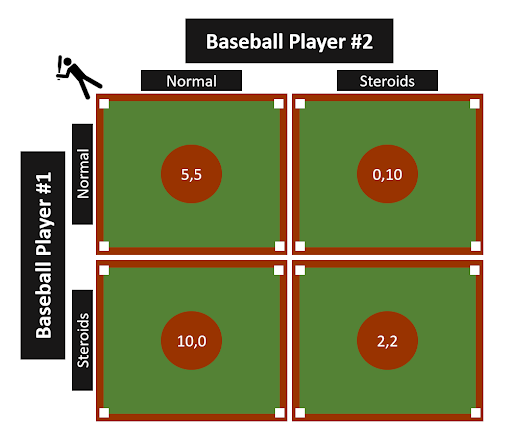
• The top left quadrant represents the scenario in which both players are fully clean and are not using any performance enhancing drugs. Both players receive a payout of 5. 
• The top right quadrant represents the scenario in which player #2 uses steroids receiving a payout of 10. Meanwhile player #1 stays clean and receives a payout of 0. 
• The bottom left quadrant is the same as the top right quadrant but with the roles reversed. Player #1 takes steroids to enhance their performance while player #2 stays clean. Player #1 receives a payout of 10 while player #2 receives a payout of 0. 
• The bottom right quadrant is the scenario in which both players choose to use performance enhancing drugs. Both players receive a payout of 2. 

There are 2 Nash equilibriums in this example, one in the top left quadrant in which both players decide to stay clean, and the other in the bottom right quadrant in which both players choose to take performance enhancing drugs.

This example highlights how players are incentivized to cheat. If a player takes steroids they have a potential payout of 10 with a worst case payout of 2 while if they decide to stay clean they have a potential payout of 5 with a worst case payout of 0. 

Baseball in the present day has created many discentives for using steroids. If we were to create a quadrant to represent this we would need to include negative payouts to represent the potential fines and suspensions that could come with taking the risk of using performance enhancing drugs. 

The Cold War

The Cold War was a period of international tension between the United States and the Soviet Union (USSR).

It consisted of a nuclear arms race, proxy warfare, and an overall competition to become the world's leading superpower. It began in the late 1940’s and lasted until the dissolution of the Soviet Union in 1991. 

While the most optimal outcome for the entire world would have been to disarm, both countries chose to build up their nuclear arsenal. 

The incentives for increasing nuclear power outweighed the incentives for disarming for both countries. If one country chose to disarm and the other continued to arm then it would have led to military inferiority. 

• The top left quadrant represents the scenario in which both the US and USSR disarm. This leads to a payout of 3 for both of them. 
• The top right quadrant represents the scenario in which the US disarms and the USSR continues to arm. This leads to a payout of 4 for the USSR and a payout of 1 for the US.
• The bottom left quadrant is identical to the top right quadrant but with the roles reversed. In this scenario, the US continues to arm and the USSR disarms. This leads to a payout of 4 for the US and a payout of 1 for the USSR. 
• The bottom right quadrant represents the scenario in which both countries choose to arm. This leads to a payout of 2 for both of them. 

In this example, there exists multi Nash equilibrium. The first equilibrium occurs in the top left quadrant in which both countries choose to disarm. The second equilibrium occurs in the bottom right quadrant in which both countries choose to continue to arm. 

Despite the most optimal payout being for both countries to disarm, in reality, both countries chose to increase their military strength. 

Through this example, we can see how both countries are incentivized to continue to build up their nuclear arsenal.

Neither country desires to take on the risk of potential military inferiority. Both countries choose a dominant strategy rather than a cooperative strategy and end up continuing the arms race. 

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Conspicuous Consumption
• Derived Demand
• Endogenous Variable
• Fiat Money
• Social Economics