Negatively Skewed Distribution
A type of distribution in which more values are concentrated on the right side (tail) of the distribution graph
What Is A Negatively Skewed Distribution?
A negatively skewed distribution, also known as a left-skewed distribution, is a distribution in which more values are concentrated on the left side of the mean than on the right side. Negative skewness has important implications on the mean, median, and mode of the data.
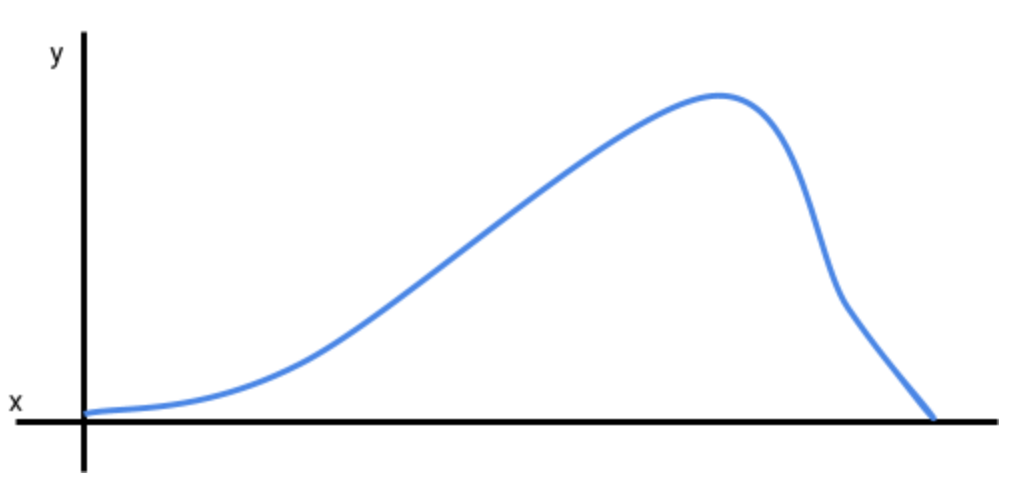
The illustration above is what a left-skewed distribution might look like. The left tail is longer in the distribution. In other words, the distribution is being pulled to the left.
In finance, a left-skewed distribution means there will likely be frequent small gains and few large losses. An investor would not want a negatively skewed return distribution because the large losses will cancel out the small gains.
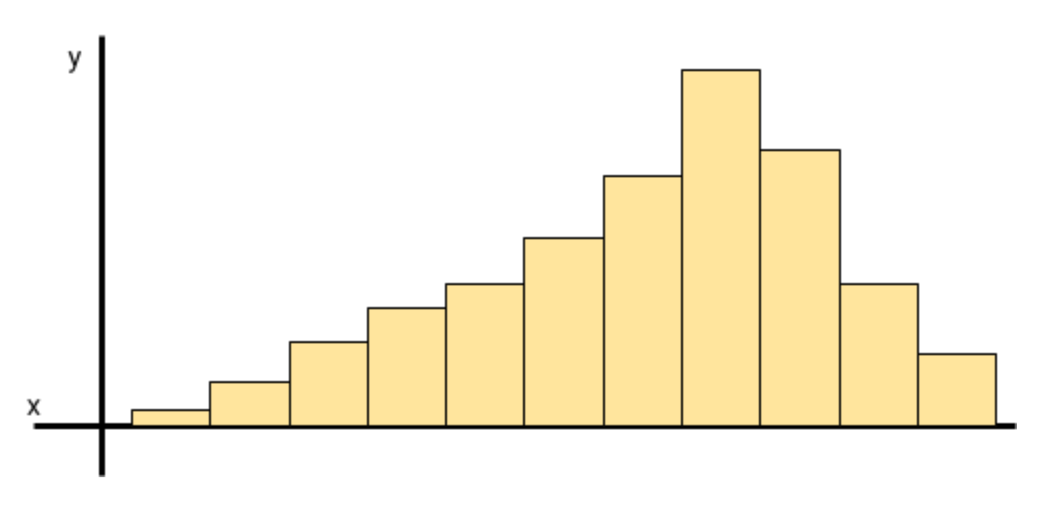
It is important to remember that a distribution may be presented in other formats, such as a bar chart or histogram. Below is a left-skewed distribution presented as a bar chart.
Key Takeaways
- A negatively skewed distribution is one that concentrates more values on the left side of the mean.
- In this distribution, the mean is less than the median, which is less than the mode, unlike a normal distribution where these are equal.
- Negatively skewed distributions in finance mean frequent small gains and few large losses, which can lead to net losses for investors.
- For example, an equity portfolio's annual returns with more frequent small gains and a few substantial losses has a negatively skewed distribution.
- Skewness measures the direction of skew (centered, positive, or negative), while kurtosis gauges how data points cluster around the distribution's center.
Central Tendency Measures in Negatively Skewed Distributions
Central tendency measures, in statistics, refer to data points representing the middle or center of a distribution. In a normal distribution, the mean, median, and mode are all equal to each other.
For example, if the mean in a normal distribution is 3, then the median and mode will also be 3. A normal distribution is also known as a bell curve.
If the distribution is skewed to the left then the mean, median, and mode will not be equal. The mean will be less than the median, which will be less than the mode.
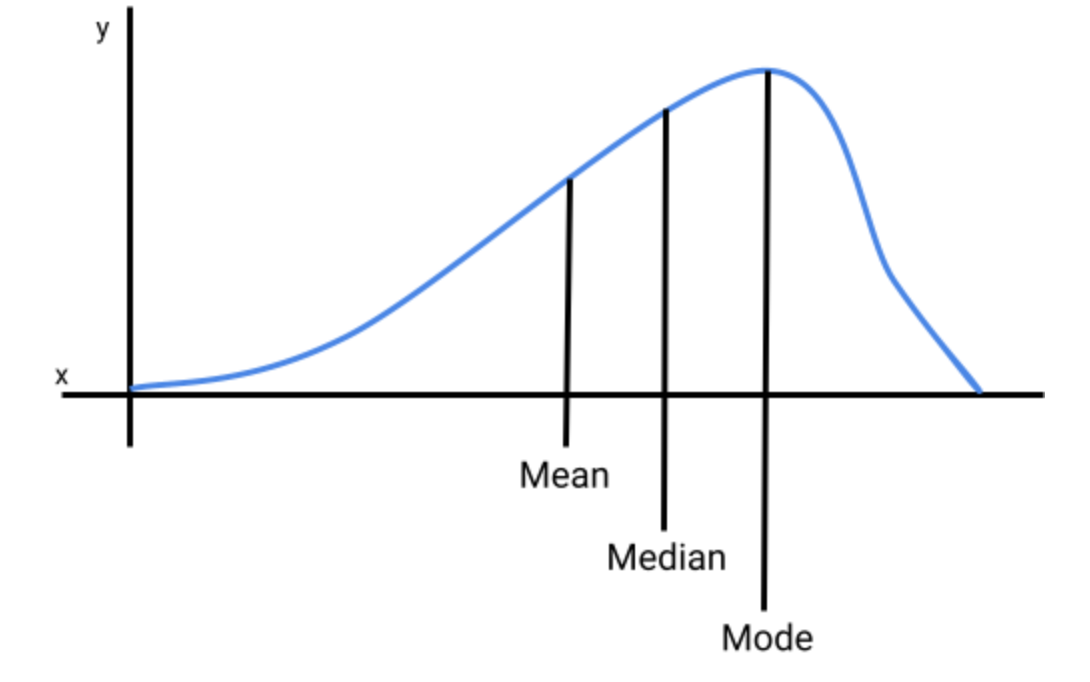
The distribution above is a left-skewed distribution where the mean is less than the median, which is less than the mode (mean < median < mode).
The table below compares the central tendency measures in each distribution.
| Distribution | Measures of Central Tendency |
|---|---|
| Positively Skewed Distribution | Mean > Median > Mode |
| Negatively Skewed Distribution | Mean < Median < Mode |
| Normal Distribution | Mean = Median = Mode |
Below is a table with definitions for mean, median, and mode.
| Measures of Central Tendency | Definition |
|---|---|
| Mean | The average of the data points: the sum of all values divided by the number of values. |
| Median | The middle point of the data set (data must be sorted in ascending or descending order). |
| Mode | The data point that appears the most in a data set. For instance, if 3 appears more times than any other number, then 3 is the mode. |
Understanding the Implications of Skewed Distributions in Finance
In finance, a negatively skewed distribution tells us that an investment or portfolio is expected to experience frequent small gains and a few large losses. On the other hand, a positively skewed distribution means that the investment is expected to experience frequent small losses and a few large gains.
A negatively skewed distribution is often less desirable because the large losses will cancel out, and likely exceed, the small gains leading to more realized losses.
In the graph below, the distribution is being pulled to the left, which means the mean return will be less than the median and mode of the return series. The mode will be the return that an investor will experience more frequently, which will be frequent small returns. Infrequent large losses will be clustered on the extreme part of the left tail, which is pulling the distribution away from its center.
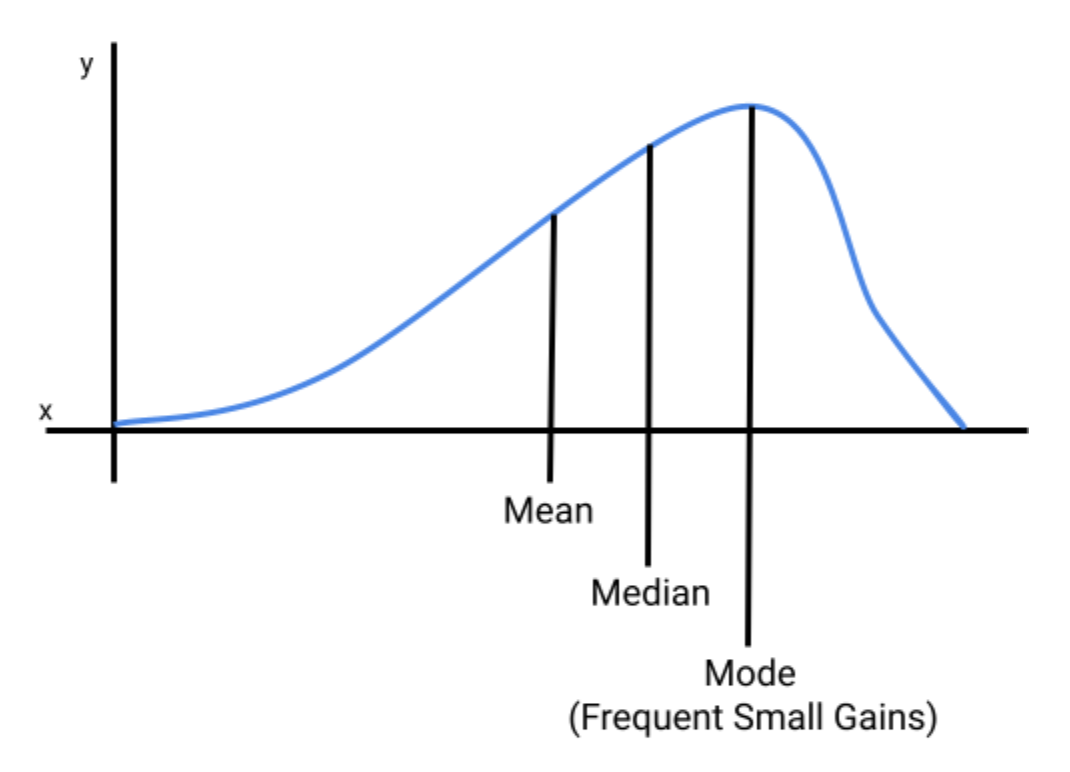
Example of A Negatively Skewed Distribution
Let’s assume that an investor wants to see the annual distribution of an equity portfolio over the past year (in the United States there are typically 253 trading days in a year). The investor proceeds to gather the annual returns and the frequency of their occurrence. The returns and the return frequency are provided in the table below.
| Returns (USD) | Frequency (Days) |
|---|---|
| -5,000 | 4 |
| -3,000 | 8 |
| -1,000 | 9 |
| -200 | 11 |
| -100 | 12 |
| 0 | 13 |
| 100 | 14 |
| 150 | 15 |
| 200 | 16 |
| 250 | 17 |
| 300 | 19 |
| 350 | 30 |
| 400 | 34 |
| 450 | 30 |
| 500 | 15 |
| 700 | 5 |
| 800 | 1 |
The investor then plots the returns and their frequencies on a graph. The vertical axis (y-axis) is the frequency (number of days), and the horizontal axis (x-axis) is the dollar amount of each return.
Below is a graph of the return distribution.
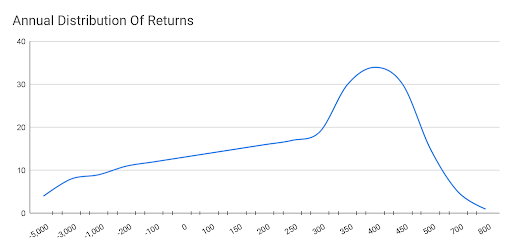
When analyzing the return series, the analyst notices that the distribution is being pulled to the left due to a few large negative returns (ranging from -5,000 to -100). Because the distribution is being pulled to the left, it is a negatively skewed distribution.
The mode of the distribution is the x-axis value which corresponds to the peak point on the graph, which is 400, and it is also the most frequent return (34 occurrences) the equity portfolio experienced over the past year.
Skewed Distributions Vs. Kurtosis
When discussing a negatively skewed distribution, in statistics, it is common to hear about kurtosis, which measures how peaked or flat a distribution is. Kurtosis measures how clustered data points are around the peak of a distribution.
The table below lists a few differences between skewness and kurtosis.
| Skewness | Kurtosis |
|---|---|
| Measures the direction of the skewed distribution. The distribution can be centered (normal), pulled to the right (positive), or pulled to the left (negative). | Measures how peaked or flat a distribution series is. |
| Measures how data points pull the distribution curve to the right or left. | Measures how data points are clustered around the center of the curve. |
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:









or Want to Sign up with your social account?