Standard Error

What Is A Standard Error?

Standard error (SE), in statistics, measures the variability of a sampling distribution, i.e., it is the estimate of the standard deviation. It measures how efficiently and accurately a sample of a distribution represents its actual population. It is a widely used measure in finance; often seen as part of regression analysis.

The sampling distribution of the mean is calculated by taking the means of random samples from the population over and over again. The distribution of the means recorded from this exercise has its own mean and variance. This square root of this variance is known as the standard error.

How To Calculate Standard Error

Mathematically, standard error is equal to the standard deviation of the distribution divided by the square root of the number of observations. The distribution of sample means usually resembles a normal distribution, based on a mean and variance.

SE can be calculated as:

SE = SD / (n)^½

where,

• SD = standard deviation of the distribution
• n = the total population

To calculate a standard error, you need the following three pieces of information:

• The number of observations (population)
• The mean, or average, of the data set
• The standard deviation

Given the equation above, we can see that to lower the error term (standard error) the population or number of observations must be increased.This is logical, as the sample mean will be closer to the population mean, as the size of the sample increases.

However, increasing the number of observations may not always be practical, and could be costly. Hence, it is important to strike the right balance between cost and accuracy.

Standard Error In Finance

Standard error is a commonly used measurement metric in finance, especially in quantitative finance, which involves the use of statistical analysis of data. It’s most prominent use is as part of regression analysis, where it is used to understand the characteristics of the population from a sample.

We go into greater detail on what SE might look like in a regression model below.

Standard Error In Regression Analysis

In regression analysis, the standard error is often referred to as the error term. It measures how far observations fall from the regression line. 

Below is an example of a regression; the orange points represent the standard error of the regression. Each orange point has a different distance from the regression line, and the SE will tell us what the standard deviation is of all the points in the regression.

Example Of Standard Error In Regression Analysis

Let’s assume an analyst would like to run a regression on the return of a market ETF and the number of cold days in a month. The data the analyst gathered is provided in the table below.

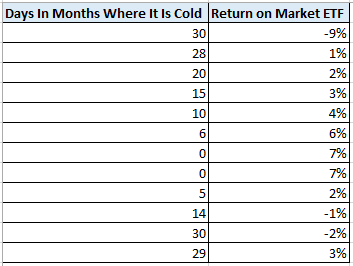
Using Data Analysis in Excel, the analyst gets the below output.

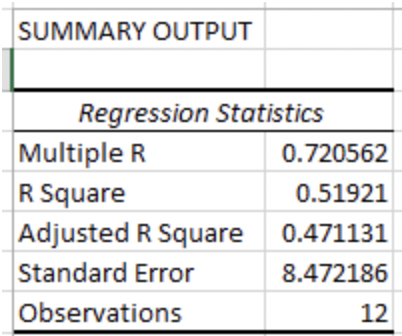
The analyst recalls that the standard error measures the average distance the monthly returns fall from the regression line. In this regression, the returns, on average, are about 8.47 standard deviations from the regression line. 

To get a better visualization of the regression and standard error, the analyst plots the regression in Excel (picture below).

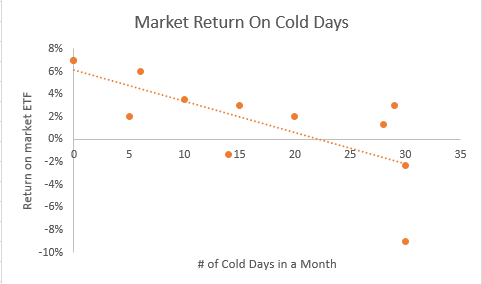
In the regression above, some of the orange points touch the line, while others are very far away; however, on average, the returns are 8.47 standard deviations away from the regression line. 

The standard error can help predict where observations will fall along the regression line. The regression above was used with 95% confidence, meaning that 95% of all returns should fall within +/- two standard deviations of the standard error.

Standard Error Vs. Standard Deviation

Standard error and standard deviation are often confused with one another because they both measure the variability of a distribution; but, the distribution that is being measured is different.

Standard error is the standard deviation of a statistical measure such as the mean. In other words, it measures how the means of a distribution are distributed amongst each other. 

For example, let’s assume an analyst would like to measure the variability of the means of three investments within a portfolio. The analyst first calculates the means of the three distributions (the vertical lines on the horizontal lines below). 

They then calculate the standard deviation of the means of the three distributions and divide the standard deviation by the square root of the size of the total population. They have effectively calculated the standard error of the total distribution.

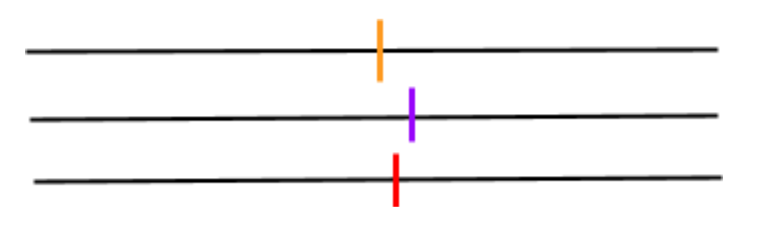
Standard deviation measures how the data is distributed around the mean of the distribution.

Let’s assume the same analyst would like to see the variability of returns for one investment over a six day investment horizon. The returns are highlighted on the number line below. 

The analyst first calculates the mean and variance of the returns, then takes the square root of the variance to calculate the standard deviation of the six returns. The standard deviation tells the analyst the variability of the returns (the data).

Standard Error Vs. R-Squared (R2)

When looking at the variability of a distribution, standard error isn’t the only metric that an analyst must pay attention to. Other statistical metrics are also looked at, one such metric is R-squared (R^2).

SE calculates the standard deviation of the observations along a regression line, while R-squared measures how well the variable we are measuring (dependent variable) can be explained by the independent variable. 

In the example where the analyst wanted to see how the market performed when there were more cold days in a month, the returns were what was being measured is the dependent variable, and the number of cold days is the independent variable.

Below is the same output from the example.

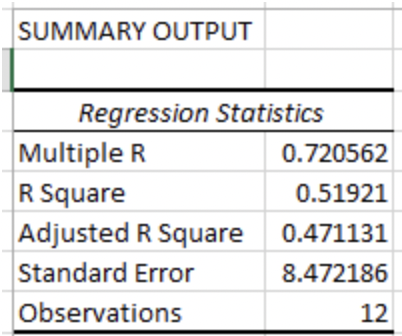
The R-square for the regression tells us that roughly 52% of the variance of returns can be explained by the number of cold days in a month.

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Retained Earnings
• Fraud Triangle
• Cost of Goods Manufactured (COGM)
• Marginal Cost Formula
• Accounts Receivable Turnover Ratio