Average Return
The arithmetic average of returns that have accrued over time
What Is Average Return?
The Average Return is the arithmetic average of returns that have accrued over time. Therefore, it's calculated by dividing the total value of returns by the total number of returns in that time period.
This method, commonly used to calculate a simple average for any set of numbers, can also be applied to calculate an average return. After adding all of the numbers together to create a single sum, the total is divided by the total number of numbers in the set.
An investor or analyst can learn what the historical returns of a stock, investment, or portfolio of companies are by looking at the average return. The average return, unlike the annualized return, does not consider compounding.
Key Takeaways
- Average Return is the simple arithmetic mean of returns over a given period, calculated by dividing total returns by the number of observations.
- To find the average return, sum up all returns and divide by the total number of observations.
- Average return helps gauge historical performance of investments, providing a basic overview of growth without considering compounding.
- Geometric averages like Time-Weighted Return (TWR) offer more precise evaluations by accounting for compounding effects and are crucial for comparing different investments over varied timeframes.
Average Return Formula
An investor or analyst can learn what the historical returns of a stock, investment, or portfolio of companies are by looking at the average return. Since the average return does not account for compounding, it is not the same as an annualized return.
To calculate, the formula is:
Average Return = Total Value of Returns / Total Number of Returns
Average Return Example
For example, let’s say the following table represents the yearly returns of some portfolios. We can calculate its average return to be 15.4%.
| Year | Return |
|---|---|
| 2018 | 15% |
| 2019 | 16% |
| 2020 | 15% |
| 2021 | 14% |
| 2022 | 17% |
(15% + 16% + 15% + 14% + 17%)/ 5 = 15.4%
If done in Excel, this calculation can be executed much quicker by applying the AVERAGE() function to the return column. For example, if this table begins in A1 and fills accordingly, the code used would be this one.
=AVERAGE(B2:B6)
Notice that the period duration is irrelevant. In this example, the years could’ve been months, quarters, or any other duration. What matters is the returns per period and the number of periods. Here’s another example.
| Period | Returns |
|---|---|
| 1 | 10% |
| 2 | 12% |
| 3 | 13% |
| 4 | 12% |
| 5 | 14% |
| 6 | 15% |
| 7 | 13% |
The average rate is calculated in the same way as before, giving 12.7%. This could’ve also been calculated with Excel’s AVERAGE() function.
(10% + 12% + 13% + 12% + 14% + 15% + 13%)/7 ≈ 0.1271 = 12.7%
Calculating Returns From Growth
If the return rates were unknown, they would need to be calculated before calculating the average return. This can be found by determining the percent change in the growth rate.
Average Growth Rate = (Ending Value / Initial Value) - 1
For example, if a stock begins the period with a $200 value and ends the period with a $210 value, its average growth rate is 5%.
Average Growth Rate = [210/200] - 1 = 0.05 = 5%
If we had a table of values instead of returns, we would have to calculate each return per period before being able to calculate the average return. Fortunately, we can either calculate the returns with the previous formula or use Excel to determine them quickly.
Here’s an example:
| Period | Initial Value | Ending Value |
|---|---|---|
| 1 | $100 | $110 |
| 2 | $110 | $115 |
| 3 | $115 | $122 |
| 4 | $122 | $120 |
We need to add a 4th column to this table to include the return rates per period. That way, the average return can be calculated.
Using Excel, we can fill that column using basic arithmetic operations. Then, that formula can be dragged down to fill out the column, resulting in this:
| Periods | Initial Value | Ending Value | Returns |
|---|---|---|---|
| 1 | $100 | $110 | 0.10 |
| 2 | $110 | $115 | 0.05 |
| 3 | $115 | $122 | 0.06 |
| 4 | $122 | $120 | -0.02 |
The code to generate that column is given by =(C2/B2)-1 in the first cell of column D, assuming that the Initial Value is in column B and the Ending Value is in column C, and then dragging it vertically downwards until the end.
These values can also be determined by hand using the previous formula as well. In any case, with this column of returns, we can then calculate the average return, which is approximately 4.8%. This value was calculated using the same method as the first two examples.
In this case, since the table is already in Excel, the AVERAGE() function was used on the return column to obtain the average return. However, its formula could have been used as well.
Limitations of Average Return
While this metric has benefits such as ease of calculation and giving a very broad summary, it’s just that. It’s meant more to provide a very quick glance at the growth rate of returns. However, this is where its benefits end.
Unfortunately, it has multiple limitations. Therefore, it should never be the only metric used when assessing growth. It should only serve as a summary while more in-depth analyses are done.
For instance, it ignores future costs that may affect profit since it focuses only on projected cash flows. Additionally, it doesn’t take into consideration the reinvestment of these positive cash flows.
This lack of accuracy implies that analysts need to use other metrics when measuring or evaluating the growth and projected behavior of returns. This is especially true when using more precise metrics based on the geometric average instead of the arithmetic average.
Note
The metric as a mathematical tool can be misleading. As the arithmetic average tends to exceed the geometric average, relying solely on the average return for growth analysis can result in an overestimation of growth.
Average Return Alternatives
As previously mentioned, while this metric has its uses, it is in no way the most ideal way to measure the growth of returns. It does not take into consideration compounding. This is why analysts also apply other metrics when assessing the returns over a given period.
One such metric is the average return via the geometric average instead of the arithmetic average. The geometric average yields a more accurate result when analyzing historical returns.
Another benefit to the geometric mean is no need for the actual amounts invested. Since it measures the returns themselves, the invested amounts are unnecessary. This eliminates the distorting effects on growth rates due to cash flows.
Time-Weighted Return (TWR)
Geometric averages also provide the benefit of comparing the performance of different investments over different periods of time. This geometric average is called Time-Weighted Return (TWR) precisely because it only considers time and not cash flows.
Time-weighted return (TWR) is used to evaluate the performance of an investment portfolio by removing the effect of external cash flows, providing a clearer assessment of investment decisions.
Its formula is as follows:

Where
- HPY = return for that period
- i = the particular period (1, 2, 3, …, n)
- n = the total number of periods
Example
If we take the values from the very first example and substitute them in this formula, we would get an average return of 15.4%. Excel can also calculate this using the =GEOMEAN() function applied to the return column.
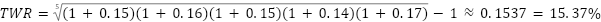
While this result can be rounded to the nearest tenth and arrive at the same 15.4% value as the arithmetic mean, the arithmetic mean is exactly 15.4%. Therefore, the geometric mean is slightly less than 15.4%.
While this might seem insignificant, it depends on the context. Small differences such as these will be quite noticeable when applied to relatively large numbers. For example, $1,000,000 at 15.4% growth is $1,154,000 whereas at 15.37% growth is $1,153,700.
The same formula or Excel function =GEOMEAN() can be applied to the other two examples, yielding 12.73% and 4.66%, respectively. Again, while these values are more similar when rounding, the geometric average is more precise.
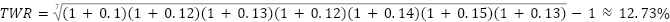
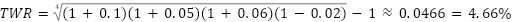
Money-Weighted Rate of Return
If an analyst wanted to take the cash flows into consideration, they would use a different geometric average called the Money-Weighted Rate of Return (MWRR).
The Money-Weighted Rate of Return (MWRR) formula is as follows:

Where
- i = the particular period (0, 1, 2, 3, …, n), with i = 0 indicating the initial investment
- n = the total number of periods
- CF = cash flows
Money-weighted return (MWRR) measures the performance of an investment by considering both the timing and amount of cash flows, providing insight into how investor actions affect overall returns.
Notice that this formula is not directly solvable for MWRR analytically due to its dependence on cash flows and underlying investment performance.
It typically requires specialized software (such as Excel or other applications) or financial tools for calculation.
Note
A thing to note about the formula is that it depends on the cash flows. This is useful when more information is provided about the returns of any given investment, payment, or other cash flow stream.
Example
The previous examples’ tables don’t possess enough information to calculate the MWRR. Here’s an example that does.
Let’s calculate the MWR of these two portfolios, each with the same funds and capital gains over a two-year period per the following table. The only difference is the timing of these invested funds.
| Return | Cashflows | |||
|---|---|---|---|---|
|
Portfolio |
Period 1 | Period 2 | Period 1 | Period 2 |
| A | 20% | 10% | $600,000 | $0 |
| B | 20% | 10% | $300,000 | $300,000 |
Let’s first determine the cash flows for the formula since there are different returns throughout the investment’s total evaluation period. Then we can find the IRR using a financial calculator. In this case, that IRR value is the MWR value.
Note
It should be noted that when reporting portfolio performance per the CFA Institute’s Performance Presentation Standards (GIPS), the average (arithmetic) return shouldn’t be included at all. Yet there are pages of directives on when to use either TWR or MWRR.
For Portfolio A:
- CF0 = -$600,000
- CF1 = $0
- F1 = 1
CF2 = $600,000 (1 + 0.2) (1 + 0.1) = $792,000
- F2 = 1
- IRR = 14.89%
Therefore, portfolio A’s MWRR = 14.56%
For Portfolio B:
- CF0 = -$300,000
- CF1= -$300,000
- F1 = 1
CF2 = $300,000 (1 + 0.2) (1 + 0.1) + $300,000 (1 + 0.1) = $726,000
- F2 = 1
- IRR = 13.40%
Therefore, portfolio B’s MWRR = 13.40%
If we were to calculate the average return of these portfolios utilizing the arithmetic mean, we would obtain a 15% between the two periods for both portfolios. Notice that this result is greater than both results obtained from calculating the MWRR.
Average Return = (20% + 10%)/ 2 = 15%
TWR and MWRR have their benefits, limitations, and clear differences between them. That being said, these are still more precise and rigorous metrics for analyzing growth than just using the average return (by arithmetic mean).
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:









or Want to Sign up with your social account?