Risk and Return
Greater risk exposure is associated with elevated return expectations
What Is Risk And Return?
A return is an increase in the value of a project, investment, or item over time. This increase in value can be expressed as a price increase or a percentage increase. A positive return shows a gain, while a negative return indicates a loss.

There are two types of returns:
- Realized return is what the term implies; it is ex-post (after the fact) return, or return that was or could have been earned. Realized return has occurred and can be measured with data.
- Expected return, on the other hand, is the less muted return from an asset that investors anticipate (expect) they will earn over some future period. As an estimated return, it is subject to uncertainty and may or may not occur.
However,
Actual return ≠ Expected return
Hence, there is always a risk attached to an investment. Return and risk move together. Risk is greater where the expectation for returns is high.
Return ∝ Risk
Key Takeaways
- Returns can be positive (gain) or negative (loss) and are expressed as either price increases or percentage increases over time for projects, investments, or items.
- There are two types of returns: Realized return (ex-post) which has occurred and can be measured, and Expected return (ex-ante) which is an estimated return subject to uncertainty.
- Return and risk are closely related; the higher the expectation for returns, the greater the risk.
- Investors aim to maximize return while minimizing risk, known as the risk-return tradeoff. Different investors have varying risk tolerance levels.
- Risk can be systematic (related to the overall market) or unsystematic (unique to a specific security). Understanding risk and return is crucial in making investment decisions.
Risk and Return Relationship
If the risk level of two securities is the same, then both must provide the same return. If the return is not the same, investors will never choose to buy more risky securities.
Investors often associate higher returns with higher risk. However, investors want to maximize return and minimize risk. This is known as Risk-Return Tradeoff.
The tradeoff between expected return and risk should prevail in a rational environment. Investors unwilling to take on risk must be satisfied with the risk-free rate of return.
In effect, investors have different limits on the amount of risk they are willing to assume and, therefore, the amount of return that can realistically be expected.
Remember that the risk-return tradeoff is ex-ante, meaning "before the fact." That is, before the investment is made, the investor expects higher returns from assets with a higher risk.
Here are some risk-return relationships for different types of investments:
| Investment | Return | Risk |
|---|---|---|
| Treasury bill | Very low | Nil |
| Bonds and debentures | Low | Low |
| Preference shares | Medium | Medium |
| Equity shares | High | High |
Do investors dislike risk? In investment, the standard assumption is that investors are rational. Rational investors prefer certainty to uncertainty.
Components of Return From an Investment
A model that explains the connection between the expected return and risk of investing in security is called the Capital Asset Pricing Model (CAPM).
This model demonstrates that a security's expected return equals the risk-free return plus a risk premium calculated using the security's beta.
1. Risk-free rate of return
The lowest rate of return that may be anticipated on an investment with no risk to the investor is known as a risk-free rate. It is the time value of money, i.e., reward for time. It is common for all types of investments.
The risk-free rate of return has three components: Inflation, Rental rate, and Investment risk.
2. Risk premium
It is the reward for assuming the risk that differs in each investment. Risk premium and risk move hand in hand. If the risk in an investment is higher, the risk premium must be higher, and vice versa.
It is necessary to generate a return above the risk-free rate to reward investors for choosing to invest in a riskier asset class. This additional return is known as the market risk premium.
Required rate of return = Risk-free rate of return + Risk premium
Total return = Rrf + β (Rm-Rrf)
Where,
- Rrf= the rate of return for a risk-free security
- Rm= the broad market’s expected rate of return
Understanding Return
Whether you're a seasoned investor or a curious novice, grasping the idea of return can provide vital insights into the potential rewards of an investment, helping you make more informed decisions.
Return on a typical investment consists of two parts:
1. Yield
When discussing inviting returns, the periodic financial flows from the investment, such as interest or dividends, typically spring to mind. For these payments, the issuer pays the asset's holder in cash.
2. Capital gain
This element is the increase (or decrease) in the asset's price, often known as the capital gain (loss). It is the difference between the asset's purchase price and the price at which it can or is sold in case of a long position.
In the case of a short position, it is the difference between the asset's sale price and the price at which the short position is ultimately closed. A gain or a loss may happen in either scenario.
Here is the formula for calculating the return:

Return on equity shares formula:
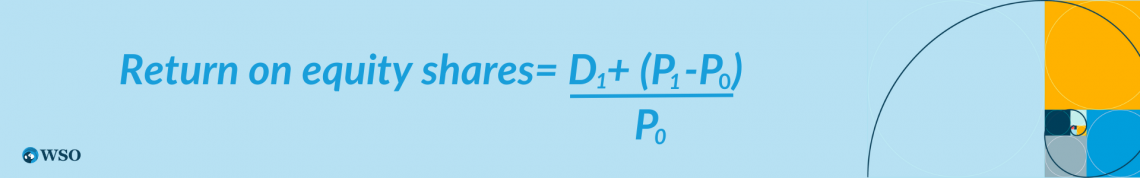
Where,
- P0 = Cost of investment at the beginning of the year
- D1 = Dividend received at the end of the year
- P1 = Cost of investment at the end of the year
What if the actual return exceeds the expected return? The disparity between a security's actual and predicted returns is known as an abnormal return.
It demonstrates whether the security has performed as expected or better. In this situation, the predicted return is often based on the Capital Asset Pricing Model.

Calculating Types of Returns
Producing a fair rate of return, we can figure out our stock investment returns by calculating and analyzing the results through the given formulas:
Average return (based on arithmetic mean)

| Year | Share Price | Dividend | Return (%) |
|---|---|---|---|
| 2012 | 118 | NIL | - |
| 2013 | 130 | 5 | (5+12) / 118 = 14.41 |
| 2014 | 120 | NIL | (0-10) / 130 = -7.69 |
| 2015 | 140 | 10 | (10+20) / 120 = 25 |
| 2016 | 160 | 5 | (5+20) / 140 = 17.85 |
| Total | - | - | 49.57 |
Average return = 14.41 - 7.69 + 25 + 17.85 / 4 = 49.57 /4 = 12.39%
Thus, based on historical data, the average annual return is 12.39%.
Limitations of arithmetic mean:
- No effect of compounding.
- A.M. may give misleading returns.
Average return (based on geometric mean)
Taking the above example, we can calculate the average return using the geometric mean method:
Average return = [(1 + R1) (1 + R2) (1 + R3) (1 + R4)]1/4 - 1
= [(1 + 0.1441) (1 - 0.0769) (1 + 0.25) (1 + 0.1785)]1/4 - 1
= (1.556)1/4- 1 = 11.68%
A.R. = [(1 + R1) (1 + R2) (1 + R3)…….. (1 + Rn)1/n] - 1
Expected return (based on probability distribution)
| Return (R1) | Probability (P1) | R1P1 |
|---|---|---|
| 30 | 0.40 | 12 |
| -20 | 0.40 | -8 |
| 50 | 0.20 | 10 |
| Total | - | 14 |
Expected return = ∑R1P1 = 14%
Return of a portfolio
Generally, an investor invests in more than one asset or security, meaning they have a portfolio.
Here is an example:
- Amount invested in equity - 40%, and the return on equity is 15%
- Amount invested in bond - 60%, and return on the bond is 10%
Then,
Portfolio return = ∑ W1R1
= 0.5 (15) + 0.5 (10) = 12.5%
Holding period return (investment horizon)
HPR is the total return earned during the holding period of investment.

Example: Mr. B initially invests in a non-dividend paying shares priced at $100. In 2013, he sold the share for $150.
Calculation of holding period return = 150 - 100/ 100 = 50%
Note
A holding period return of 50% is earned over 10 years. It is not 50% per year.
Effective annualized return (EAR)
EAR is the equivalent per annum return.
EAR = (1 + RT)1/T - 1
Where,
- RT = holding period return
- T = holding period in years
Example: Mr. B initially invests in a non-dividend paying shares at $100. In 2013, he sold the share for a price of $150.
Calculation of holding period return = 150 - 100/ 100 = 50%
The investor who earns 50% return over 10 years earned 4.13% per year:
EAR = (1 + 0.50)1/10 - 1 = 4.13% per year
Note
People typically use the effective annualized return to make an effective investment decision.
Absolute Return vs. Risk-Adjusted Return
Absolute return is the total return generated by an investment without considering the risk of an investment. It is not the best measurement to compare the investment alternatives as they have different risks.
Risk-adjusted return is a relative measure of return as it is expressed per unit of the underlying risk. Methods used for calculating it are Sharpe's ratio (return to volatility ratio), Treynor’s ratio, etc. The higher the Sharpe ratio, the better the security in terms of a risk-return relationship.
You should consider both the risk taken and the returns created by the investments when comparing the performance of two investments or checking your portfolio's returns. You can measure the same thing using risk-adjusted return.
It is a theory that assesses the amount of risk taken to earn a return to calculate the return on investment. Comparing multiple individual equities, mutual funds, and portfolios using risk-adjusted returns is helpful.

Example: Stock A returned 12% over the past year with a standard deviation of 10%, and Stock B returned 10% with a standard deviation of 7%. The risk-free rate over the period was 3%. The Sharpe ratios would be calculated as follows:
- Stock A: (12% - 3%) / 10% = 0.9
- Stock B: (10% - 3%) / 7% = 1
Even though Stock A had a higher return, Stock B had a higher risk-adjusted return, meaning that it gained more per unit of total risk than Stock A.
Understanding Risk
Risk is often associated with the dispersion, or the variability, in the outcomes. Risk is assumed to arise out of variability, which is consistent with our definition of risk as the chance that the actual outcome of an investment will differ from the expected outcome.
If an asset's return has no variability, it has no risk.
All investors are risk averse to an extent; everyone wants higher returns for every additional unit of risk and tries to avoid unnecessary risk. There are two types of factors affecting risk:
- External factors
They include social and economic factors. Some examples include economic policies, taxation, political conditions, cultural changes, social changes, foreign effects, etc. - Internal factors
They influence the return of that specific security, which internal factors control. Some examples include management, labor conditions, efficiency, governance, etc.
Common stocks exhibit the greatest return variability (dispersion) compared to other assets, while small common stocks exhibit even more variability.
The variability of corporate bonds is substantially lower, resulting in the distribution of returns being more uniform.
The annual returns for bills are evenly distributed. Investors should be willing to purchase a particular asset if the expected return compensates for the risk.
It is easy to say that investors dislike risk, but more precisely, we should say that investors are risk-averse. A risk-averse investor will not assure risk simply for its own sake and will not incur any given level of risk unless there is an expectation of adequate compensation for doing so.
We have said that investors would like to maximize their returns. They will never choose to minimize their risk. The reason is that there are costs like lowering an expected return to reducing risks.
Types of Risks
Risks are an intrinsic part of any financial activity, and understanding the diverse types of risks is crucial for both experienced investors and those new to the field.
Let's start by defining total risk, a concept in finance that refers to the combined risk associated with all the various factors that can affect the value of an investment.
This encompasses both systematic risk, associated with market-wide factors, and unsystematic risk, specific to individual assets or companies.
The formula for total risk can be expressed as:
Total risk = Systematic Risk + Unsystematic Risk
From this, it follows that there are two primary categories of risk: systematic risk and unsystematic risk, each encompassing different aspects of potential uncertainty in investments.
1. Systematic risk
This is the total risk caused by factors beyond the controls of a specific company.
- Non-Diversifiable risk.
- Beta (β) is an indicator of systematic risk.
Types of systematic risk are as follows:
a. Market risk
This is caused due to the tendency of investors to follow the directions of the market. Therefore, market price changes are the most prominent source of risk.
Market index ∝ Share price of company
b. Interest rate risk
This arises due to changes in the market interest rate. It has two opposite components: Price risk and Reinvestment risk.
Note
Price risk is connected to shifts in a security's price brought on by interest rate movements. Bond prices have an inverse relationship with interest rates.
Reinvestment risk refers to the danger of reinvested dividend income. When market interest rates decline, it occurs. The investor will then be able to reinvest his interest and dividend income at a lower rate, which suggests a reduced future is coming.
It is essential to recognize that when interest rates drop, bond prices increase, but reinvestment risk increases.
Market Interest rate ∝ 1/ Fixed income securities
c. Purchasing power risk (inflation risk)
This arises due to inflation. It erodes the purchasing power of money. If an investor’s income does not increase with the rising inflation, then investors will be getting lower income.
Note
Fixed-income securities have a high level of inflation risk. However, equity is a good hedge against inflation.
Example: An investor invests in a 5-year 10% bond at a par value of $1000. At the end of the year, the inflation rate is 5%. In this case,
Interest income in nominal terms = $100 (i.e., 10% of 1000)
However, income in real terms = 100/ 1 + 0.05 = $95.23
At the end of the year, $100 will buy goods and securities worth $95.23, as available at the beginning of the year.
d. Exchange rate risk
This is the uncertainty associated with changes in the value of foreign currencies. It affects only MNCs or companies which use imported raw materials or products.
2. Unsystematic risk
This is caused by factors within the control of a specific company related to management, assets, labor, or capital. It is a diversified risk you can avoid if you build a diversified portfolio by investing in companies from different industries or economic sectors.
Types of unsystematic risk are:
1. Business risk
This arises due to fixed operating costs in a company’s cost structure, which include labor unrest, inefficient management, and corporate governance.
2. Financial risk
It arises due to the presence of fixed financial costs in a company measured by financial leverage. It is associated with capital structure.
Calculating Risk
Grasping how elements like variance, standard deviation, covariance, correlation coefficient, and beta assist in estimating risk is crucial. It's important to understand different products (with different features) available in the market, and their risk-return aspects should not be ignored.
Methods for calculating risk:
1. Range
A range is a difference between the highest and lowest possible return on an investment. The higher the range, the greater the dispersion and risk.
2. Variance or standard deviation
In the case of only return series is given:
S.D. = √(x - x̄)2/ n
Example:
| Year | x (Return) | (x- x̄)2 |
|---|---|---|
| 1 | 10 | 1 |
| 2 | 12 | 9 |
| 3 | 8 | 1 |
| 4 | 5 | 16 |
| 5 | 10 | 1 |
| ∑x̄ | 45 | 28 |
X̄ = mean return = 45/ 5 = 9%
S.D. = √28/ 5 = 2.36%
In case a probability distribution of returns is given:
S.D. = √Pi (Ri - E (R))
Example:
| Ri | Probability (Pi) | RiPi | Pi(Ri - E(R)) |
|---|---|---|---|
| 20 | 0.1 | 2 | 6.4 |
| 15 | 0.2 | 3 | 1.8 |
| -5 | 0.2 | -1 | 57.8 |
| 10 | 0.3 | 3 | 1.2 |
| 25 | 0.2 | 5 | 33.8 |
| ∑RiPi | 12 | 101 |
E(R)= Expected return = 12%
Total risk= S.D. = √101 = 10.05%
Risk Formulas
Dividing risk into its two components, a general (market) component, and a specific (issuer) component, we have systematic risk and unsystematic risk:
Systematic risk formula
An investor can construct a diversified portfolio and eliminate part of the total risk, like the diversifiable or non-market. What is left is the non-diversifiable portion or the market risk.
Variability in a security's total return is directly associated with the overall movements in the general market, otherwise known as systematic risk.
This can be captured by the sensitivity of security’s return concerning the market return. This sensitivity can be calculated by the beta (β) coefficient.
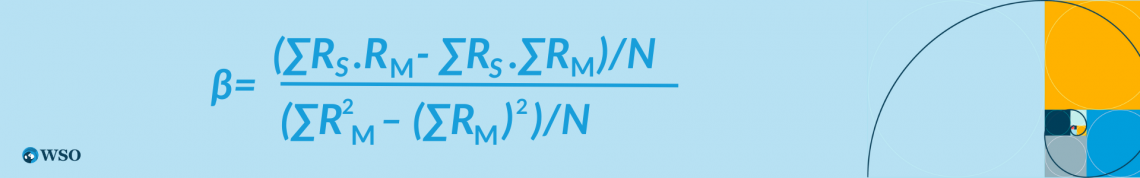
Where RS is the return on the security, RM is the market return, and β is the indicator of systematic risk.
- If β = 1, security is as risky as the market index.
- If β < 1, security is less sensitive than the market index, which is the defensive stock.
- If β > 1, security is riskier than the market index, which is the aggressive stock.
Example:
| Security return(RS) | Market return(RM) | RS.RM | RM2 |
|---|---|---|---|
| 10 | 8 | 80 | 64 |
| 12 | 10 | 120 | 100 |
| 15 | 12 | 180 | 144 |
| 30 | 25 | 750 | 625 |
| 6 | 4 | 24 | 16 |
| 4 | 5 | 20 | 25 |
| Total = 77 | 64 | 1174 | 974 |
β = 1174 - 77 × 64/ 6 ÷ 974 - (64)2/ 6 = 1.21
It must be noted that ß can also be negative. If security has negative B, it implies that its returns are moving in the opposite direction of the market return.
Note
When the market returns increase, the security returns decrease, and vice versa. This may be the case for certain stocks for some periods.
Unsystematic risk formula
The variability in a security's total returns unrelated to overall market variability is called the nonsystematic (non-market) risk. This risk is unique to a particular security and is associated with such factors as business, financial, and liquidity risks. Although all securities tend to have some nonsystematic risk, it is generally connected with common stocks.
Total risk = systematic risk + unsystematic risk
Hence,
Total variance = Systematic variance + Unsystematic variance
Therefore,
Unsystematic variance = Total risk - Systematic variance
Conclusion
Return and risk go together in investments. Indeed, these two parameters are the underlying basis of the subject. Everything an investor does is tied directly or indirectly to return and risk.
The two parts of return are yield and price change. Risk is the other side of the coin. Therefore, risk and expected return should always be considered together.
The primary components of risk are interest rate, market, inflation, business, exchange rate, and liquidity risk. The term return can be used in different ways. It is important to distinguish between realized return and expected return.
An investor cannot reasonably expect larger returns without being willing to take on more risks. Consider the investor who wishes to avoid any practical risk on a nominal basis.
Such an investor can deposit money in an insured savings account, earning a guaranteed return of a known amount.
However, this return will be fixed, and the investor cannot earn more than this rate. Although the risk is effectively eliminated, the chance of making a larger return is also reduced.
If investors wish to earn a return larger than what the savings account provides, they must be willing to take risks, which holds uncertainty.



or Want to Sign up with your social account?