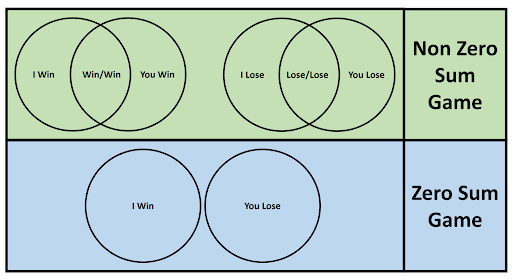
Zero Sum Game (and Non Zero Sum)

What Is A Zero-Sum Game?

A zero-sum game is a situation in which the total amount of all the players' gains minus the total amount of all the players’ losses is equal to zero. It also includes any kind of competition where one party's gain is another party's loss.

In a zero-sum game, the total amount of value, wealth, or payoff is limited. If one player within a game increases their value, then the other players in the game lose value. This creates a situation called Pareto Efficiency (also known as Pareto Optimality) in which an individual is unable to better themselves without another individual losing. 

These games are a fundamental concept within game theory. Game theory is the study of how rational individuals make decisions in everyday life through the lens of various mathematical models. When game theory first began it applied exclusively to zero-sum games, though as the field continued to develop it expanded to account for alternative situations. 

Let's take an example in which there are two dogs and three tennis balls. Both dogs would like to have the maximum amount of tennis balls possible. In this game, there are two players (the dogs) and there is a limited good (the tennis balls). 

In a scenario in which one dog is able to take all three of the tennis balls. Dog #1 would have three tennis balls while dog #2 would have zero. In a mathematical equation this would be mapped out as a positive three and a negative three. Those two values cancel each other out and the sum becomes zero. 

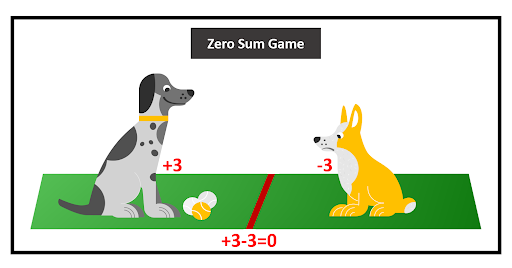
Scenarios like this one occur in everyday life all of the time. In the world of economics which can be loosely defined as the study of how we as a society allocate limited resources, the concept of zero-sum games is important to understand.

Zero-sum games in everyday life

Certain submarkets within the financial market can be categorized as zero-sum. The markets often referred to as zero-sum are those involving futures contracts and options contracts. When the buyer of an option gains, the seller of the option loses.  

This same concept can be applied to a number of sports, board games, and children's games. 

• When a football team wins, the other team loses. At the end of the National Football League season, if you add up all of the wins acquired by every team and then you add up all of the losses acquired by every team, they will cancel each other out resulting in zero. 
• Monopoly is a zero-sum game in which a limited amount of real estate is available to be divided up amongst the game's players. The game ends when one player is able to acquire ownership of all the available real estate on the board, this player is the winner and the other players lose. 

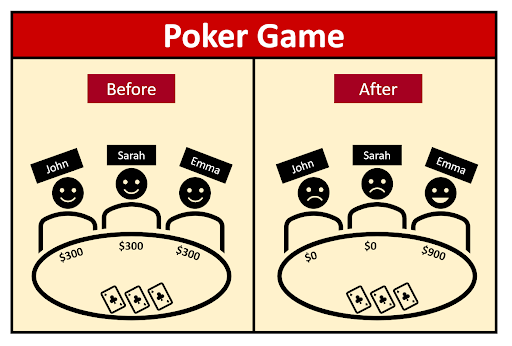
• When two kids play rock, paper, scissors together the result is zero-sum. If player #1 puts out his hand and shows paper while player #2 puts out his hand and shows rock, then player #1 wins and receives a payout of positive one. Meanwhile, player #2 loses and receives a payout of negative one. These two values cancel each other out resulting in a sum of zero.

Mercantilism was the dominant economic policy and theory from the 16th century to the 19th century. The economic philosophy that was fundamental to the policies that were implemented at the time was based on zero-sum concepts. 

People believed that the amount of value in the world was fixed and therefore the only way to acquire more wealth was to take it from another country. This ideology led to the imposition of tariffs and imperialism.

• When it came to trade, countries emphasized the pursuit of trade surpluses as opposed to trade deficits. The main goal was to export goods in exchange for gold and silver. Governments would discourage foreign imports and promote domestic manufacturing and production. 
• Many conflicts arose between competing countries due to the belief that the amount of wealth in the world was limited. In the 17th and 18th centuries, the Anglo-Dutch wars occurred. In the 17th century, the Franco-Dutch war ensued from 1672 to 1678. All of these wars were driven by mercantilist theories. 
• The world evolved from mercantilism to capitalism when Adam Smith, David Hume, and Jean Jacques Rousseau began to develop new economic theories. 

Zero-Sum games in a payoff matrix

Matching pennies is a theoretical zero-sum game, used within game theory. There are two players and each player has a penny. 

Each player secretly chooses whether to have the penny turned to heads or tails. After each player has made their selection they simultaneously show each other their pennies. 

• If the pennies match then player #1 receives player #2’s penny. 
• If the pennies do not match then player #2 receives player #1’s penny.

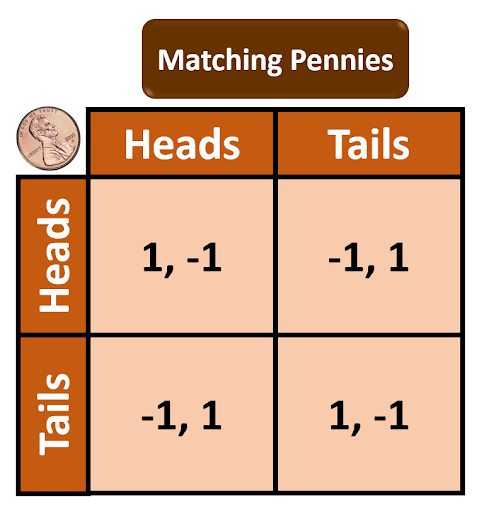
Matching pennies is a great example. When one player wins and the other player loses, the winning player finishes the game with two pennies while the losing player finishes the game with zero pennies. The positive gain of one and the negative loss of one cancel each other out resulting in a sum of zero. 

For a long time, economists have used the matching pennies game to analyze how individuals make decisions. If the game has multiple rounds instead of one round, players will often attempt to develop a strategy while simultaneously attempting to figure out what the opponent's strategy is. The intention of the economist when analyzing the results is to understand how people make choices within a zero-sum competition.

Battle of the sexes is a game theory proposed by R. Duncan Luce and Howard Raiffa in 1957. It centers around two individuals coordinating a time to meet up and attend an event together. 

In this theory, there are two events. Both players prefer to attend an event together as opposed to alone. But when it comes to each player's specific preference for the event they should attend, they cannot agree. 

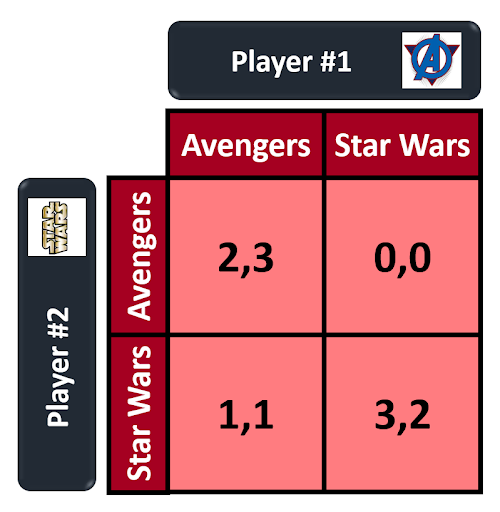
This payoff matrix illustrates the payoffs that will occur for each potential scenario. Player #1 prefers to see the new Avengers movie while player #2 prefers to see the new Star Wars movie. Both players' main priority is to see a movie together.

• In the top left quadrant we see the scenario in which both players see the Avengers. Player #1 receives a payout of three while player #2 receives a payout of two. Player #1 receives a payout of three because in addition to getting to see the movie with their partner, they as well get to see the movie they want to see.  Player #2 receives a payout of two because despite not seeing the movie they wanted to see, they still got to see a movie with their partner. 
• In the top right quadrant we see the scenario in which player #1 goes to see Star Wars and player #2 goes to see the Avengers. Both players end up seeing a movie alone and both players do not go to their desired movie. This results in a payout of zero for the both of them
• In the bottom left quadrant we see the scenario in which player #1 goes to see the Avengers and player #2 goes to see Star Wars. While both players went to a movie alone, they both got to see their desired movie. This results in a payout of one for the both of them. 
• In the bottom right quadrant we see the scenario in which both players see Star Wars. This results in a payout of two for player #1 and a payout of three for player #2. Player #1 receives a payout of two because despite not getting to see the Avengers, they still get to see a movie with their partner. Player #2 receives a payout of three because they are able to see both their desired movie alongside watching it with their partner. 

This example details how a game can be non-zero-sum. In this scenario neither player wins at the expense of the other player. Both players have the intention to work together and coordinate the most optimal strategy for the group. 

Non-zero-sum games

Games are not always zero-sum, often they can be non-zero-sum. A non-zero-sum game can occur when there is a net benefit or even potentially a net loss. In this scenario, value is created or destroyed as opposed to zero-sum games in which value is exclusively transferred. 

A positive-sum game is a version of a non-zero-sum game. In a positive-sum game value is created. If we add up the payouts from winning and subtract the payouts from losing we end up with a sum that is greater than zero. Players within a positive-sum game may cooperate to create a mutually beneficial outcome. 

• An example of a positive-sum could be a stock that is rising in value. If every player buys the stock and then sells it at a higher price, value is consistently created resulting in a positive-sum game.
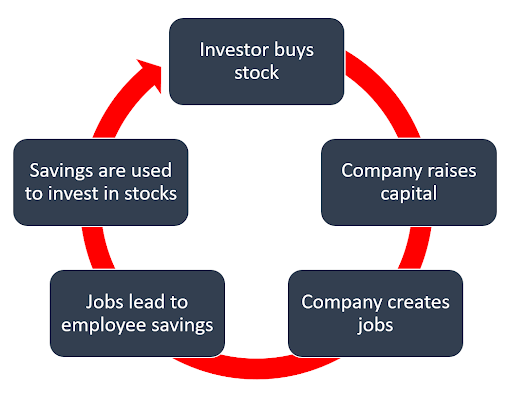
• Another example of a positive-sum game is long-term investing. When an individual purchases a stock this allows a company to raise capital through selling equity. The company is able to use this capital to create more jobs. Employees working for the company receive a paycheck and use some of the money to put towards their savings. The savings can then be used to invest through purchasing stock. This process creates value for the economy.

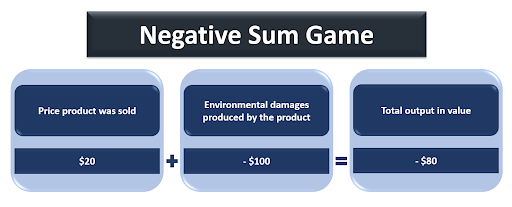
A negative-sum game is another version of a non-zero-sum. In a negative-sum game, value is destroyed. If we add up the payouts from winning and subtract the payouts from losing ,we end up with a sum that is below zero. 

• An example of this occurring in daily life could be a war between two countries. Despite one country winning the war and the other losing, both countries end up worse off than they were prior to the war. This is called a Pyrrhic victory. When this occurs it is a negative-sum game. 
• Another example could be if a company sells a product that causes environmental damage. On a macroeconomic scale, there is a positive payout produced by the product being sold, but also a negative payout produced by the environmental damage. If the negative payout is larger than the positive payout then the value is lost which is a negative-sum game. 

Positive-sum games create the opportunity for win-win situations. Negative-sum games create the opportunity for lose-lose situations. Players that are participating in a non-zero-sum game will often have both conflicting interests and shared interests. 

If cooperation and trust can be integrated into a game then oftentimes a positive-sum game is created. If trust and cooperation cannot be achieved, it may lead to a negative-sum game in which value is destroyed. 

In the above example, both individuals share the common interest of moving the couch. If trust can be established and cooperation can be had then a positive outcome can be produced.  

• In the win-win scenario both individuals are able to work together to establish trust. They are able to cooperate and lift the couch together leading to a mutually beneficial outcome. 
• In the lose-lose scenario both individuals have a desire to move the couch though refuse to work together. Trust is not established and cooperation is not achieved. This leads to the couch going unmoved which is a negative outcome for the both of them 

Sometimes in business, two companies are able to work together to create a mutually beneficial outcome that is greater than the outcome that would have been produced had both companies chosen to work separately. 

Synergy is a business phenomena in which two companies combine their strengths together to produce a greater payoff than that which would have been achieved independently. The opportunity to create and provide more value is one of the main incentives underlying a push for a merger or acquisition.  

Synergy is a positive-sum game and a win-win scenario. Value is created through cooperation and teamwork. Both companies come out the other side more profitable than before. 

A merger offers the opportunity for two companies to integrate their technologies, their workforce, and their supply chains. This leads to an increase in gross profit via cost reduction and elevated operational efficiency. 

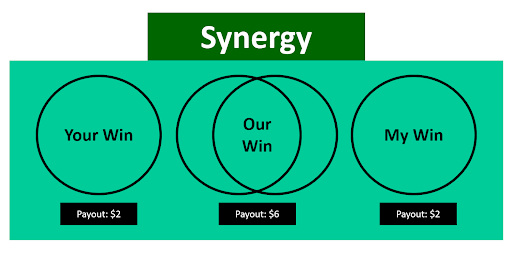
In the above example, two companies are able to come together to produce a higher payout. 

Both companies can receive a payout of $2 independently. However, working together they can receive a payout of $6, which split evenly results in a $3 payout for both companies. 

Social and economic implications

Zero-sum and non-zero-sum games have profound social and economic implications. All trades that occur are by definition a non-zero-sum. This is because when two individuals decide to make a trade, they are doing so because they both believe it is more beneficial to make the trade as opposed to not making the trade. This concept permeates all economic exchanges. 

Through technological innovation, we are able to create new and more efficient products and services. Through international trade, we are able to create competitive advantages that lead to higher quality products that are sold for lower prices. This leads to an economy that is constantly growing and this growth leads to a higher standard of living over the long run. 

^{Photo taken from the Federal Reserve}

The transformation from mercantilism to capitalism led to an evolution in economic thinking. Prior to capitalism it was believed that the amount of wealth in the world was fixed. 

Post capitalism, it was discovered that the amount of wealth in the world could grow. This revolution led to massive societal changes that occured within a relatively short time period. 

• The percentage of people who live in poverty used to be over 89%, now it is under 9%.
• Since 1848 the average person's real income has increased from between 2,500% to 5,000%.
• If the world had a fixed amount of wealth, then as the population increased from 1 billion in 1800 to 6.1 billion in 2000 the world would have become less affluent and not more. 

The idea that there is a fixed amount of wealth in the world is sometimes called the fixed pie fallacy. This relates directly to the lump of labor fallacy which states there is a fixed amount of work to be done within an economy. 

Zero sum thinking or zero sum bias refers to the cognitive bias humans inherently have in which they perceive a situation to be zero sum. It can cause us to improperly assess specific situations as a gain for ourselves and a loss for another or vice versa. It can as well lead us to becoming more competitive as we attempt to maximize our resources. 

This cognitive bias can be attributed to evolutionary psychology. Pre-capitalism and especially in hunter-gatherer tribes, resources were limited. The community had to effectively distribute resources amongst its members. 

If a disproportionate gain went to one individual, there was a proportionate loss for another individual. In addition, technological advances were slow so it was very unlikely that an individual would witness economic growth within their lifetime. 

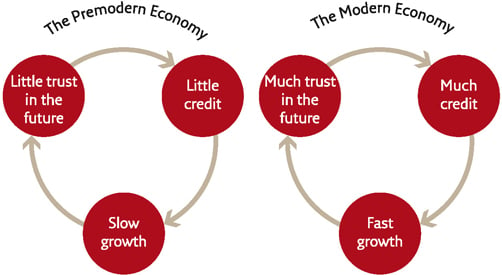
While people used to believe that the level of production was fixed, nowadays we are able to emphasize innovation and progress in order to increase production. By placing more trust in the future, we are able to fund projects with the potential to increase the total amount of wealth in the world. 

• “Over the last 500 years, the idea of progress convinced people to put more and more trust in the future. This trust created credit; credit brought real economic growth, and growth strengthened the trust in the future and opened the way for even more credit.” - Yuval Noah Harari

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Econometrics
• Financial Economics
• Margin Analysis
• Market Structure
• Nash Equilibrium