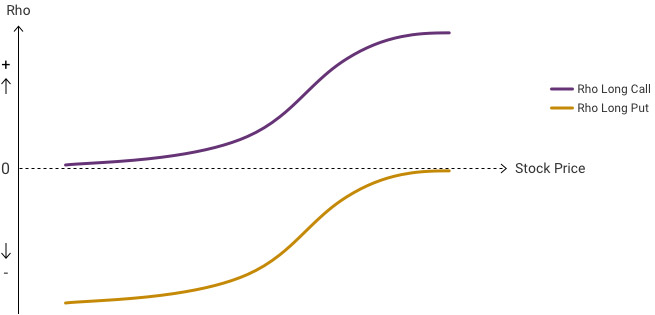
Rho (ρ)

What Is Rho?

Rho (⍴), one of the Greeks, represents the value an option will lose or gain with a 1% change in the risk-free rate (which, in most cases, is the U.S. Treasury bill rate). It measures an option's sensitivity to changes in the risk-free rate of interest.

Interest rates can impact an option's value as they alter the cost of carrying the position over time. An investor should consider the cost of capital. 

As this effect is applicable to cost over time, interest rate changes impact longer-term options much more than options near expiry. 

A higher stock price and longer time until expiration generally mean greater sensitivity to changes in interest rates, equating to higher absolute rho values.

Rho is positive for long calls, increasing with the stock price, and it is negative for long puts, approaching zero as the stock price increases. It is positive for short puts and negative for short calls.

It is considered the least important and least used of the Greek option metrics and is typically expressed in a dollar amount. This metric shows how much money an option can gain or lose if the risk-free interest rate changes by 1%. In most cases, the U.S. Treasury bill rate acts as the risk-free rate.

This metric may also refer to the aggregate risk exposure to a change in the interest rate for a portfolio of several options positions.

For example, if an option has an ⍴ of 1.5, then for every 1% increase in interest rates, an increase by 1.5% in the value of the option occurs. Options are most sensitive to interest rate changes when they are at the money and have a long time to expire.

Rho Calculation

The exact formula for ⍴ is complicated. However, it is calculated as the first derivative of the option's value with respect to the risk-free rate. 

It measures the expected change in an option's price for a 1 percent change in the risk-free rate.

For example, a call option is priced at $5 and has a ⍴ of 0.35. If the risk-free rate rises by 1 percent, e.g., from 2 percent to 3 percent, the call option value would rise from $4 to $4.35.

Generally, a call option's price increases as interest rates increase, and a put option's price decreases as interest rates increase. Thus, call options have positive ⍴, while put options have negative ⍴.

Assume that a put option is priced at $10 and has a ⍴ of -0.55. If interest rates were to decrease from 3 percent to 2 percent, then the price of this put option would increase from $10 to $10.55. In the same scenario, assuming the call option mentioned above, its price would decrease from $4 to $3.65.

⍴ is larger for options in the money and decreases continuously as options change to become out-of-the-money. Also, it decreases as the expiration time decreases. 

Long-term equity anticipation securities (LEAPs), which are options that have an expiration date greater than one year away, are much more sensitive to changes in the risk-free rate. Thus, they have a ⍴ larger than that of shorter-term options.

⍴ is a primary input in the Black–Scholes model, with a change in interest rates having a minor overall impact on options pricing.

Rho in Practice

This Greek is expressed as the amount of money an option will lose or gain with a 1% change in the risk-free rate. Essentially, it measures an option's sensitivity to changes in the risk-free rate of interest.

This Greek is considered the least important and least used of the Greek option metrics and is typically expressed in a dollar amount, even though it shows how much money an option can gain or lose if the risk-free interest rate (in the U.S., the interest rate paid on U.S. Treasury bills) changes by 1%.

For example, if an option has an ⍴ of 2, then for every 1% increase in interest rates, an increase by 2% in the value of the option occurs. Options most sensitive to interest rate changes are at-the-money and have the longest time to expiration.

Rho Example

Let us assume that interest rates have increased from 1% to 2%. Now, let us suppose that a long call option is comfortably in the money with a ⍴ of just 0.05 and a price of $1.50. 

Given the 1% increase in interest rates, the value of the call option has increased from $1.50 to $1.55, which we would get by adding the ⍴ of 0.05 to the current market price of $1.50.

On the other hand, if an investor deals with long put options and interest rates increase from 1% to 2%, the put price will likely decrease. 

For example, if the ⍴ of the put option is -0.55 and the current value of the put option is $2, we will assume that, given a 1% increase in interest rates, the put option value will fall to $1.45.

Types of Rho

Following are the various ways this Greek can be used while options trading:

Positive ⍴

Rho is positive for long calls as higher interest rates increases call premiums.

Long calls grant the option to buy stock. The cost of that right is less than the fully exercisable value and is called the premium. 

The discrepancy between the premium and the option's value can be deposited into an interest-bearing account. This makes call options an excellent choice for some.

For Example: 

Assume ABC has a current market price of $500

Buying Stock: Buy 1000 Shares of ABC at $500 per share = $50,000 Total Cost ($500 x 100 Shares) 

Buying Call Option: Buy 1 $500 Call at $750 Premium = $750 Total Cost  

The total exercisable value for this option is $50,000 (right to buy 100 shares at $500). Therefore, the cost to purchase the option ($750) is less upfront capital than the total exercisable value. 

The remaining $49,250 could be deposited and earned interest or invested and earned a return. This will be positively reflected in the value of the long call option due to the increase in interest rates.

Negative ⍴

Rho is negative for puts purchased, as higher interest rates decrease put premiums.

A long put gives the right to sell shares at a predetermined price in exchange for the option's premium. When short-selling a stock, an alternative to puts, the seller receives the proceeds from the sale that could be deposited into an interest-bearing account. 

This makes long puts less favorable than the alternative (short-selling) in a high-interest rate environment.

For Example: 

ABC has a current market price of $500

Shorting Stock Value: Sell 100 XYZ at $50 per Share = $50,000 Total Proceeds ($500 x 100 Shares) 

Buying Put Option: Buy 1 $500 Put at $750 Premium = $750

The total exercisable value for this option is $50,000 (the right to sell 1000 shares at $500). 

The cost to purchase the option ($750) is more upfront capital than the proceeds the total exercisable value would generate in an interest-bearing account. 

The $50,000 from the short sale could be deposited and earn interest. This is why rho negatively affects the value of a long put option as interest rates change.

positive and negative rho in detail

An interest rate increase will also increase the value of long options (calls) and decrease the value of short options (puts). Therefore, long puts and short calls have a negative ⍴, and long calls and short puts have a positive ⍴.

However, rho is not a factor that ordinarily affects option prices significantly. Interest rates tend to shift option prices only when there is a significant and unexpected change in the risk-free rate. 

For example, if a public announcement were made following a Federal Open Market Committee (FOMC) meeting that the Fed is decreasing the prime lending rate by a quarter of a percent and the decrease in rates was unexpected – then rho would likely have a significant impact on option prices. 

However, it would be in line with the overall market impact of such an unexpected rate change, which would most likely lead to increased market volatility, which, in turn, creates higher option prices.

Interest rates and changes in them commonly impact options (reflected in the value ⍴) as the option's expiration date approaches. 

Additionally, Long Term Equity Anticipation Securities options, because of their longer timeframe, are more sensitive to a change in interest rates than regular options, which have a shorter lifespan.

Types of Options

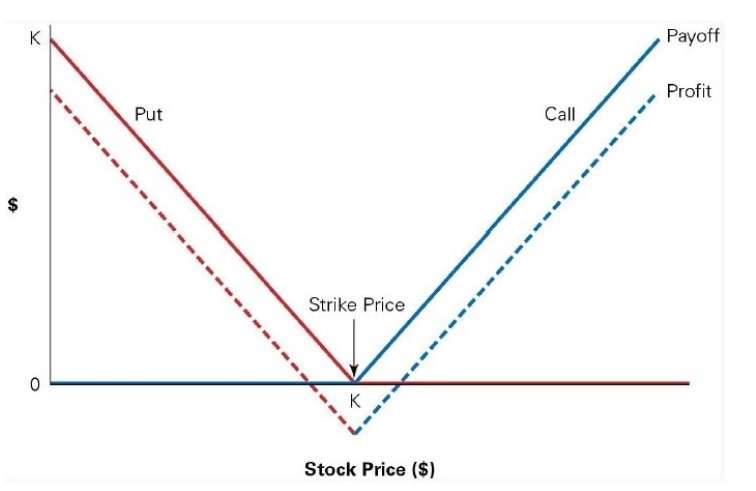
The concept of the intrinsic value of an option contract is straightforward. It means how the strike price (agreed price in an option contract) correlates to the stock's market price and vice-versa. The relationship between the strike price and the market price will decide whether an option contract will get exercised.

In-the-money (ITM), at-the-money (ATM), and out-of-the-money (OTM) entail different price outcomes depending on whether the option is a put option or call contract. 

The general rule of thumb is that in-the-money favors the buyer, while out-of-the-money favors the seller of the option contract. In-the-money means the option will provide a profit and, thus, gets exercised, while out-of-the-money means the option contract will provide a loss if exercised and, thus, expires worthless.

Let us examine the three primary option conditions in relation to rho:

1. Out-of-the-Money (OTM)

These options are either put options with a strike price that is lower than the market price or call options with a strike price above the current market price of the underlying stock. 

Out-of-the-money options do not have an intrinsic value. Instead, they have time value, as the market price may rise or fall, possibly moving the option in the money before expiration. ⍴ is low for well out-of-the-money options.

2. At-the-Money (ATM)

These options have a strike price that is the same or virtually the same as the underlying asset's current market price. Call and put options at the money may simultaneously increase in value, especially if the underlying stock's future price trend is perceived as uncertain or volatile. 

In such a case, ⍴ may indicate whether the underlying stock's future price trend is more likely to be bearish or bullish. The option that catches the most interest from investors is probably the one that will most likely pay off.

3. In-the-Money (ITM)

These options have intrinsic value to the extent that their strike price is in the money: the strike price of a put option above the market price or a strike price of a call option below the current market price. Whatever profit they would produce if exercised right now is the intrinsic value.

They also have time value, as the strike price may become deeper in the money before the option expires. Rho values are the highest for options with a strike price either at-the-money or in-the-money.

Why Do Interest Rates Affect The Price of an Option?

The only time rho is considered important is when the interest rates change significantly. Interest rates impact the value of calls due to the carrying cost of holding financial instruments like stocks. 

The carrying cost of holding such financial instruments is based on the funds required to purchase them. The funds required may need to be borrowed, in which case an interest cost would be associated. 

Even if the money required was available, an opportunity cost would be associated because that money could have been invested into an interest-bearing security. Therefore, the higher the interest rates, the higher the carrying costs.

Buying calls on a financial instrument is cheaper than buying it due to the opportunity cost previously mentioned, so the carrying cost is then built into the call price. Due to this, as interest rates increase, the call price also increases as the increased carrying cost of holding the security is reflected in the price.

Furthermore, calls become more attractive as interest rates increase. This is because the cost savings effect between buying calls and buying the underlying security becomes more pronounced. 

This is because there is a potential for a more significant return for investing cash in interest-bearing securities. This leads to increased demand for calls which also increases the call price.

Overall, the ⍴ Greek does not have much effect on the option price, which is why it is considered one of the least significant Greeks.

Researched and authored by Rohan Kumar Singh | LinkedIn

Free Resources

To continue learning and advancing your career, check out these additional helpful WSO resources:

• Auction Market
• Naked Call
• Close
• Day Trading
• Primary Market