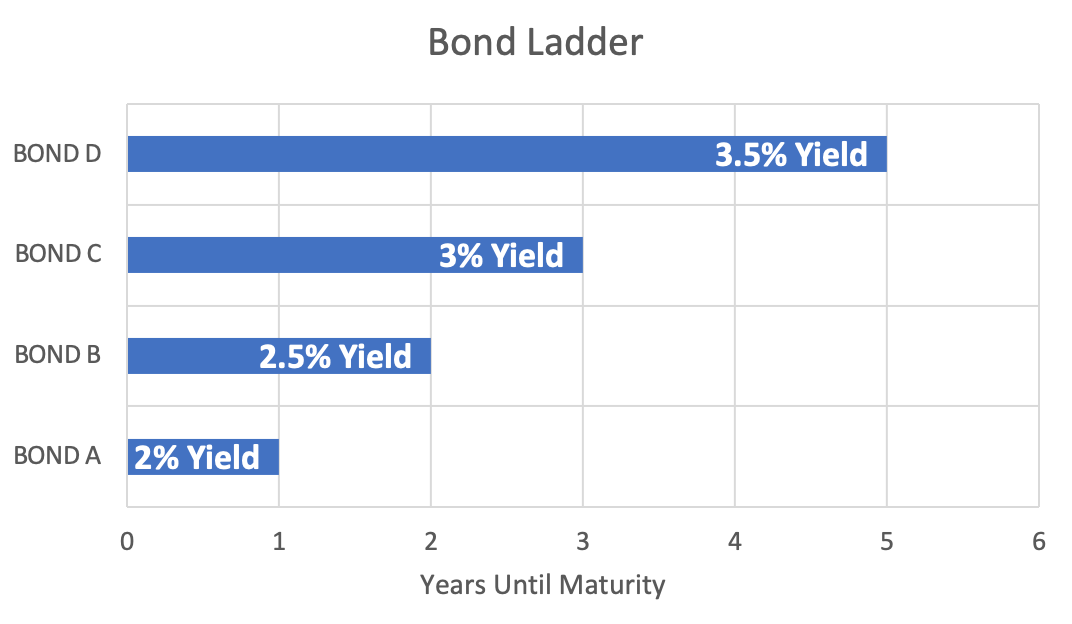
Bond Ladder
It is a strategy for fixed-income investors looking to reduce price sensitivity in their portfolio as a whole due to interest rate risk
What is a Bond Ladder?
Developing a bond ladder is a strategy for fixed-income investors looking to reduce price sensitivity in their portfolios due to interest rate risk. Creating a ladder is also a strategy to structure cash flow more consistently.
There are a few key ideas to understand why this strategy is effective:
- By investing in bonds that mature at different dates rather than multiple bonds that develop during the same year, changes in interest rates will not affect the entire portfolio equally. This is because price sensitivity depends on the maturity of a bond.
- By staggering bond maturity dates, principal repayments are more frequent than if the bonds were to mature simultaneously. This gives investors more flexibility and locks up more significant portions of capital for shorter periods.
These core concepts are based on the specifics of a bond's payment structure as it reaches maturity and how investors calculate bond valuation.
Key Takeaways
- A bond ladder strategy involves purchasing bonds with staggered maturity dates to reduce price sensitivity to interest rate fluctuations and create a consistent cash flow stream.
- The bond ladder strategy empowers investors to navigate market dynamics effectively, offering resilience, income consistency, and overall investment success through careful planning, monitoring, and adaptation.
- A deep understanding of bond valuation and pricing mechanisms is crucial for optimizing portfolio performance and income generation through systematic reinvestment of maturing bonds.
- By diversifying across bond maturities, investors can mitigate interest rate risk and enhance portfolio stability while maintaining flexibility and liquidity.
Bond Structure and Valuation
Bonds are an example of a fixed-income asset with specified payments in the contract. For example, a bond contract includes the par value (also known as the principal), coupon rate, maturity, and specifications on repayment frequency.
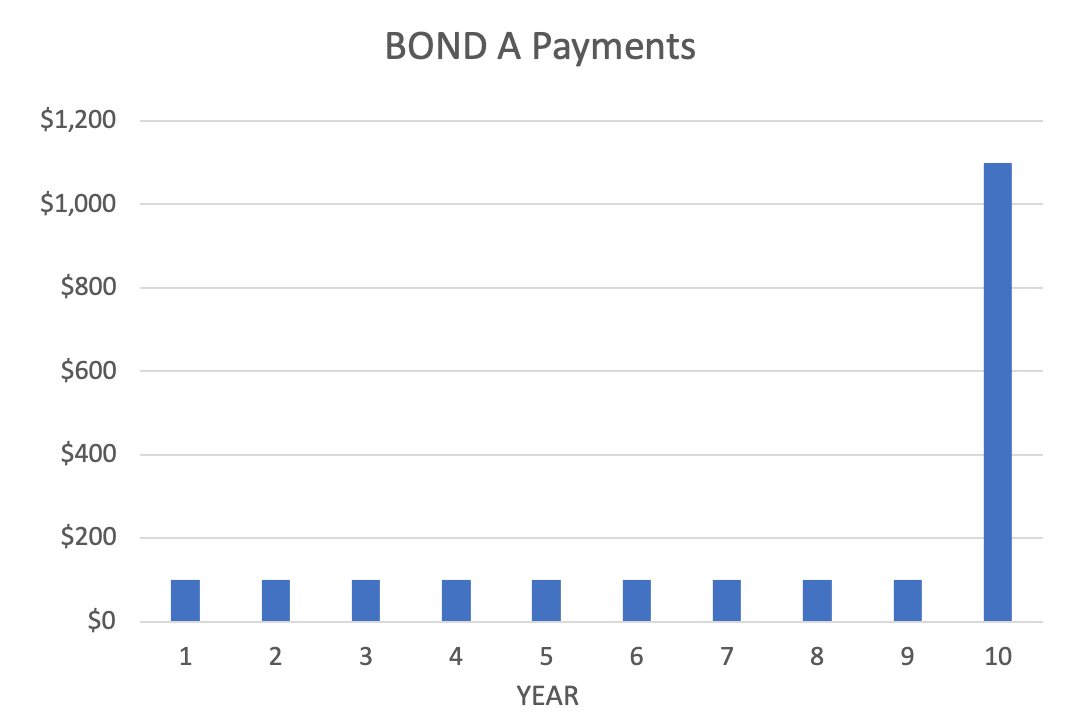
The par value is the amount of money an individual loans the bond issuer. Examples include governments and corporations issuing bonds to finance expenditures with debt. The principal is repaid once the bond matures, along with the final coupon payment.
The coupon rate determines the amount of money each coupon or fixed payment is worth. For example, a 5% coupon on a bond with a principal of $1000 would be $50.
Coupon Payment = Coupon Rate x Principal
The maturity is the time until the principal is repaid to the investor. For example, a maturity of 7 years would mean that the investor can expect coupon payments for the next seven years, along with the par-value.
Repayment frequency is how often the investor will receive coupon payments. The coupon payment is typically annual but can also be semi-annual or quarterly. In this case, the coupon payment would be divided by the number of periods per year.
Coupon Payment = (Coupon Rate / Periods per Year) x Principal
As is the case with valuing future returns for most assets, we must consider the time value of money to determine the price of a bond.
If you ask anyone, the decision between receiving $100 now vs. $100 in ten years is quite simple. Although the money now is sure, there is no guarantee of receiving money ten years from now.
In addition to the uncertainty of the future, inflation, and interest rates reduce the present value of money in the future. For example, we assume a 2% annual inflation rate, that $100 has 2% less purchasing power each year.
This means for each year into the future, your money can buy fewer products, even if you have the same nominal dollar amount!
To get around this problem, we discount the future payments to determine their present value with the following equation:
Present Value = Future Value/(1 + r)n
We know that a bond offers a series of fixed payments over time. The bond's present value is the sum of the current value of all these payments. This is typically synonymous with the price of the bond.
Coupon1/ (1 +r)1 + Coupon2/ (1 +r)2 + Coupon3/ (1 +r)3 + ...+ Couponn/ (1 +r)n + Principal/ (1 +r)n
If the bond price were higher than the value of those payments, people would not buy, lowering the price. But conversely, if the price were lower than the value of those payments, the cost would rise with the increase in demand.
Note
As bonds mature within the ladder, the principal can be reinvested at prevailing interest rates, providing a steady income stream.
This leaves one important question. What value should be used for the discount rate, allowing us to solve for the present value? Investors' required rate of return determines the discount rate. This is because the discount rate is equivalent to the yield to maturity or annual return on the investment if held until the bond matures.
How do investors formulate their required rate of return? First, investors think about what rate of return they can get without any risk and then add premiums for any added risks the investment has.
Required Rate of Return = Risk-free Rate + Risk Premiums
If there were no premiums for added risk, investors would opt not to invest. Instead, they would invest in the less risky alternative, offering the same return without added risk.
A few examples of risk premiums are essential for determining the required rate of return in a bond. These include:
- Default risk premium
- Maturity risk premium
- Liquidity risk premium
For bonds more likely to default, coupon payments and the principal repayment are deemed less specific. As a result, a premium for this added risk is called the default risk premium. The difference in bond yield concerning default risk is called the credit spread.
The maturity risk premium is associated with the time until maturity. This is because a more extended period until maturity means more time for interest rates to change, impacting the risk-free rate. Why does this matter?
Changes in the risk-free rate affect the entire yield curve and can make a bond lose value, as newer bonds offer a higher yield for less risk. To capture interest-rate sensitivity, this premium is also included in the price of a bind.
Liquidity risk is a premium added to bonds that do not have an ample supply or demand. As a result, exiting the position is difficult, especially when default seems likely. For this reason, an extra premium is added.
How does Bond Ladder work?
Understanding bond pricing and its relation to discount rates gives us the core tools to appreciate why a bond ladder is an effective strategy.
The main takeaway is that creating a ladder removes the impact of maturity length on price sensitivity from changing interest rates.
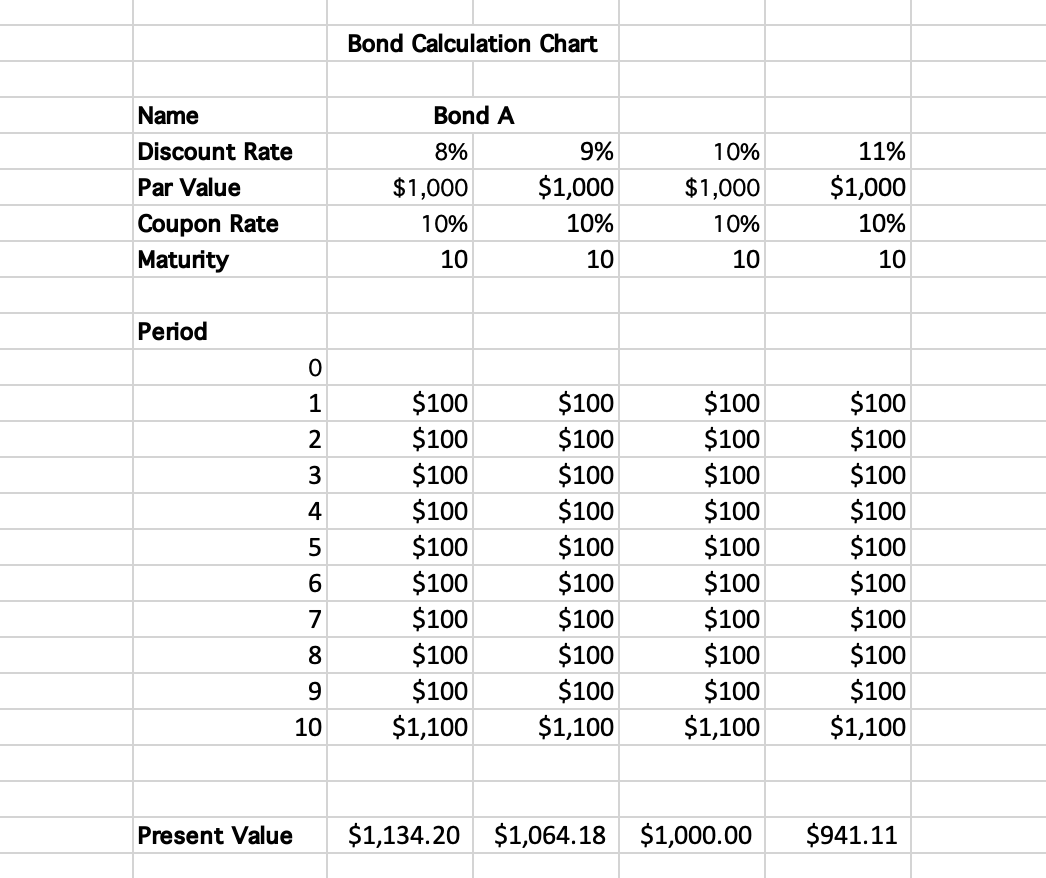
Looking at our formula for determining a bond's price, we see that the discount rate is in the denominator of all the terms we add. Therefore, an increase in the discount rate would lower the price, while a rise in the discount rate would reduce costs.
To make the comparison simple, let's compare two portfolios of bonds. The first portfolio has a group of bonds, all expiring in 10 years, while the second portfolio has bonds expiring in 1 year, five years, and ten years.
How do the prices of the two bond portfolios compare with changes in interest rates? Let's say the central bank increases the target for the federal funds rate, raising it by 100 basis points. At this point, the entire yield curve would be shifted by 1% as the risk-free rate increases.
Because the risk-free rate increases, the investor's required rate of return also increases by 1%. This means that the present value of future cash flows is now lower than before the rate hike, as we are discounting them more steeply.
The effect of this discount is much more significant for the first portfolio, as all of the bonds are maturing further in the future. This is because of the compounding effect of discounting as given by the present value formula.
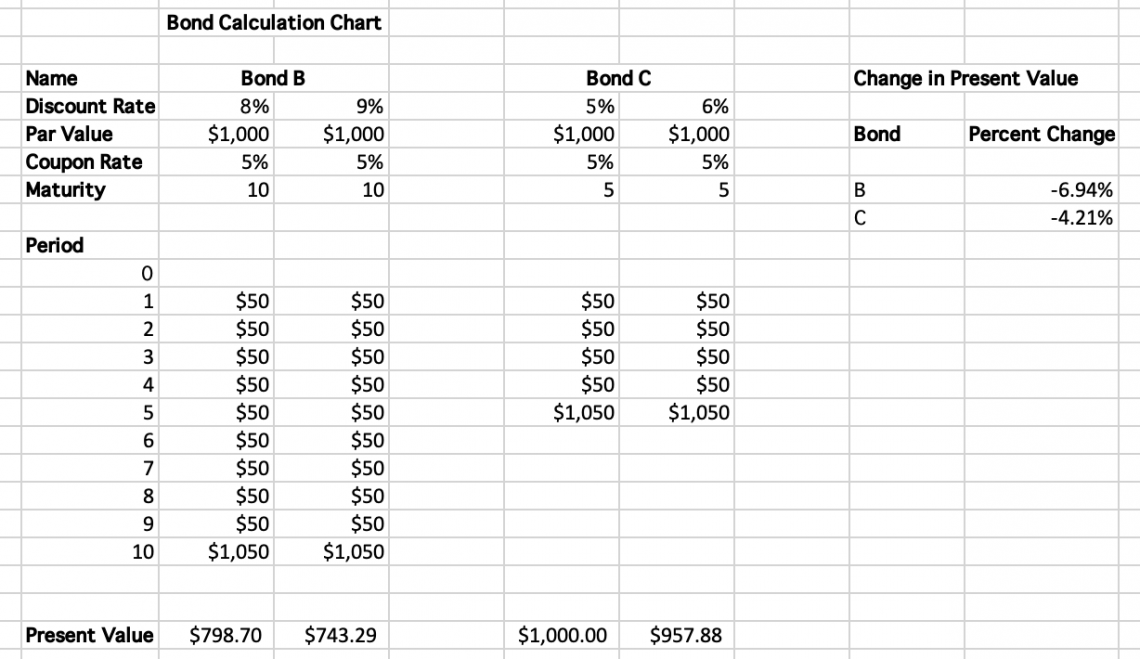
Compare the discount on the principal repayment for both of these bonds: Principal/ (1 +r)1 vs Principal/ (1 +r)5
Assuming the principal repayment and the discount rates are the same, we can see the discounting effect is more influential on the present value of the bond expiring in 10 years. This is what is known as interest rate sensitivity.
Because the first portfolio comprises bonds expiring in 10 years, the price will shift dramatically for all bonds. However, in the second portfolio, the impact on the cost of changing rates will be less profound, as some bonds are closer to maturity than those in the 10-year maturity grouping.
The thinking behind creating a bond ladder is that it smoothes out the fluctuations in interest rates in the portfolio.
For bonds close to maturity, we can purchase new long-term bonds offering higher yields with principal repayments due to increased interest rates. This helps to offset losses in the value of existing long-term bonds, which just decreased in value from rising interest rates.
The thinking is the same for when interest rates decline. New bond purchases will have lower yields. However, longer-term bonds in the portfolio will have increased in value.
Essentially, we will have more frequent fixed payments by creating a ladder. This allows us to reinvest at higher rates when our portfolio declines and see capital gains when yields fall.
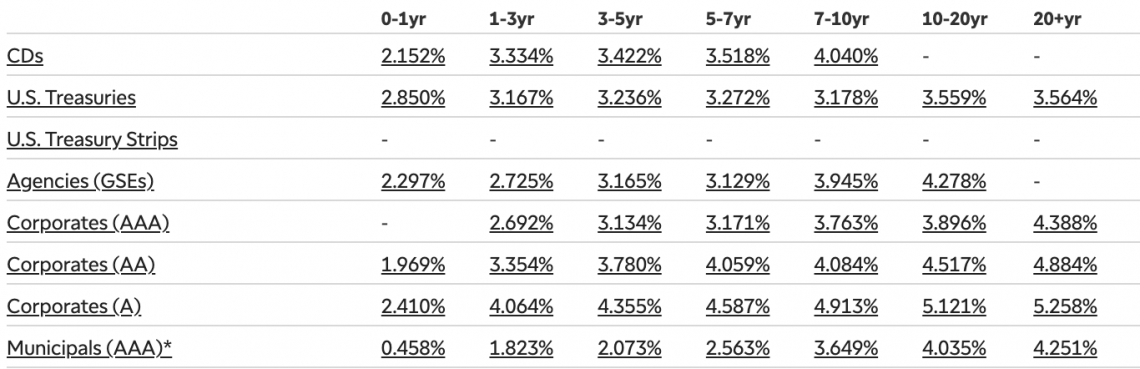
The portfolio's overall yield will be the average of the yields locked in at different investment times, offering a more consistent return to investors.
Another positive of a bond ladder's more consistent cash flow is the ability to take advantage of other opportunities.
As in portfolio one, if an investor has only a portfolio of long-term bonds, they will have their money locked up until maturity if they want to keep the rate of return from the time of their investment without having to worry about the possibility of capital losses.
How To Create A Bond Ladder?
When creating a ladder, there are a few different components to consider. These will impact income generation and the risk associated with the ladder.
These include:
- Rungs
- Spacing
- Material
The ladder rungs are the different coupon payment dates and maturity dates. The number of rungs is determined by investor preference and their chosen investment amount.
For an investor looking to invest $10,000, they can create ten rungs of equal portions of $1000. It is also possible to have rungs of different weights, although this could increase risk.
Considerations some investors have when creating rungs are coupon and maturity dates. By staggering the dates of these rungs, coupon payments become more consistent.
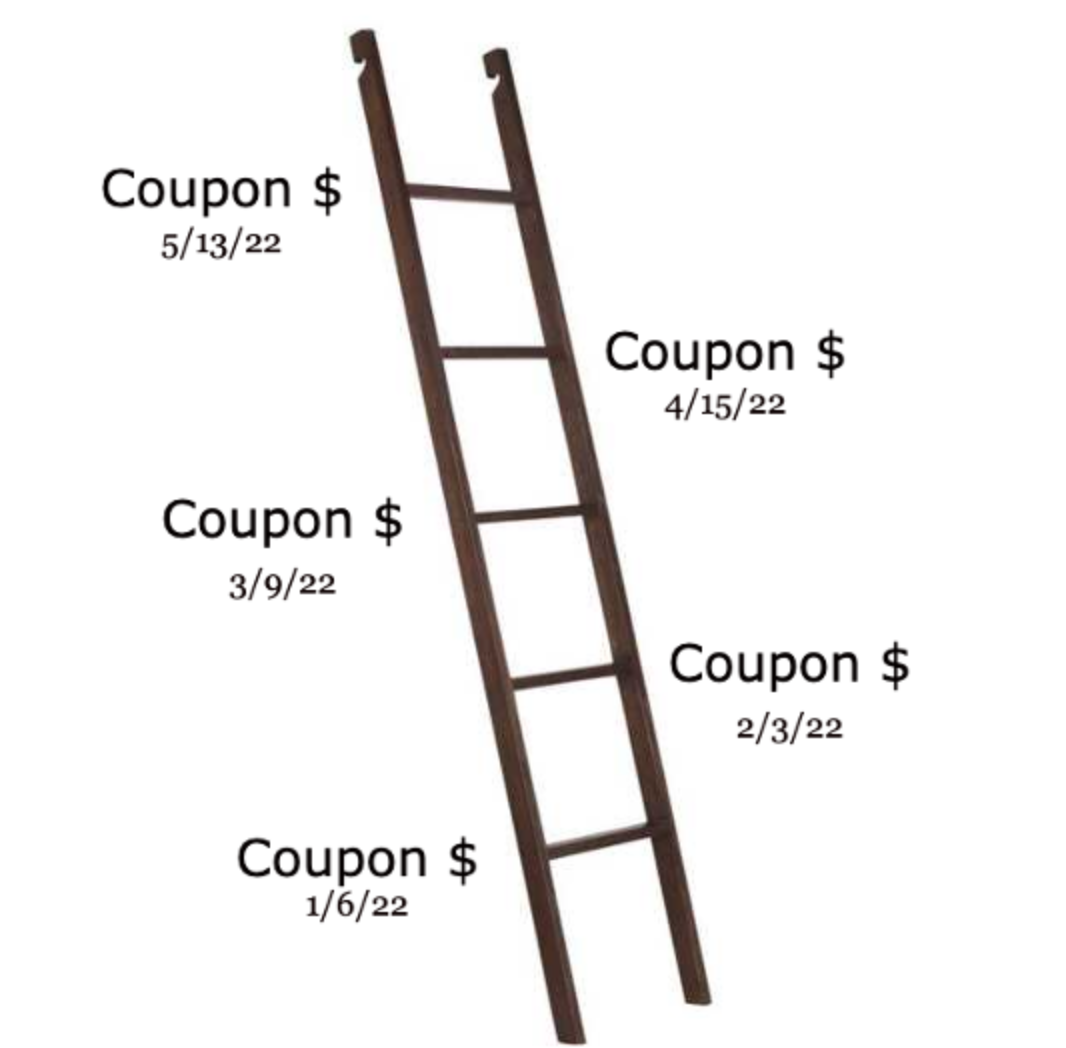
For example, with just six semi-annual coupon payment bonds, it is possible to have a monthly income from coupon payments. Spacing refers to how far apart the bond maturities are. Equal spacing is considered to be the less risky option, but once again, it is up to investor preference.
With bonds spaced further apart, investors can take advantage of the higher yields of longer-term bonds. The downside to this is less consistent principal repayment.
The material of the bonds is precise about what type of bonds are being invested in. Because creating a bond ladder is a risk management tool, it is common for investors to choose investment-grade bonds compared to risky bonds with a higher likelihood of default.
How To Build A Corporate Bond Ladder?
Building a corporate bond ladder involves several steps to create a diversified portfolio with staggered maturity dates. Below is the guide for the same:
1. Define Investment Objectives: Start by clearly defining your investment goals, risk tolerance, and time horizon. Understand your income needs, liquidity requirements, and desired level of portfolio diversification.
2. Research and Selection: Conduct thorough research on corporate bonds available in the market. Consider factors such as credit rating, issuer stability, industry sector, and bond characteristics (coupon rate, maturity date, call provisions).
3. Establish Maturity Structure: Typically, corporate bond ladders span multiple years, with bonds maturing at regular intervals (e.g., one year, two years, three years, etc.). Choose the number of rungs (maturities) based on your investment horizon and income needs.
Note
As bonds mature within the ladder, the proceeds can be reinvested at prevailing interest rates, providing a steady income stream.
4. Allocate Capital: Allocate your investment capital across the selected corporate bonds according to your predetermined maturity structure. Ensure proper diversification by spreading investments across different issuers, industries, and credit ratings.
5. Purchase Bonds: Execute purchases of selected corporate bonds to establish the initial ladder. Pay attention to prevailing market conditions, bond prices, and transaction costs.
6. Monitor and Rebalance: Regularly monitor your corporate bond ladder to track bond performance, interest rate movements, and credit risk. Rebalance the ladder periodically by reinvesting proceeds from maturing bonds into new bonds with similar maturities.
7. Manage Cash Flows: Manage cash flows generated by maturing bonds within the ladder. Reinvest principal repayments into new bonds to maintain the ladder's structure and income stream.
8. Review and Adjust: Conduct periodic reviews of your corporate bond ladder to assess its performance, risk exposure, and alignment with investment objectives.
What Is The Purpose Of Bond Ladder Strategy?
The purpose of a bond ladder strategy is to manage fixed-income portfolios systematically. By purchasing bonds with staggered maturity dates, it aims to balance risk. Diversifying across different maturities helps mitigate interest rate fluctuations.
This strategy also aims to provide a consistent income stream. As bonds mature, investors receive principal repayments, ensuring stability. This cash flow can be reinvested or used for income needs, particularly beneficial for retirement planning.
Moreover, a bond ladder offers flexibility and liquidity. With regular maturing bonds, investors can reinvest or access cash as needed.
This adaptability allows for adjustments to meet evolving financial goals effectively. Overall, it optimizes returns, generates income, and provides stability in fixed-income portfolios.
Advantages Of Bond Ladder
Bond laddering provides investors with a structured approach to managing fixed-income portfolios, offering benefits such as enhanced diversification, consistent income streams, and increased flexibility. Some of them are explained below:
1. Diversification: Bond laddering spreads risk across different maturities, reducing exposure to interest rate fluctuations. This diversification can enhance portfolio stability.
2. Income Stream Management: With staggered maturities, bond ladders provide a consistent income stream as bonds mature periodically, allowing investors to reinvest at prevailing interest rates.
Note
The ladder can be tailored to meet specific cash flow needs, such as funding retirement expenses or upcoming large expenditures.
3. Liquidity: Having bonds maturing at regular intervals provides liquidity, as investors can access cash without selling bonds at potentially unfavorable times.
4. Risk Mitigation: By holding bonds to maturity, investors can mitigate interest rate risk compared to bond funds, where prices fluctuate with market rates.
5. Flexibility: Investors can adjust the ladder by adding new bonds or adjusting maturities to align with changing financial goals or market conditions.
Disadvantages Of Bond Ladder
Despite its advantages, bond laddering has drawbacks that investors need to consider, including reinvestment risk, limited yield potential, and higher transaction costs. Some of the drawbacks are explained below:
1. Reinvestment Risk: During periods of declining interest rates, reinvesting proceeds from maturing bonds may result in lower yields, potentially reducing overall income.
2. Limited Yield Potential: Bond ladders may not offer the highest potential yield compared to other fixed-income strategies, such as bond funds or individual bond selection.
Note
The structure of a bond ladder can also contribute to a smoother reinvestment of matured bonds, providing more stability and potential protection against significant changes in interest rates.
3. Higher Transaction Costs: Managing a bond ladder requires periodic purchases and sales, incurring transaction costs that could erode returns, especially for smaller portfolios.
4. Market Risk: While individual bonds held to maturity may not be subject to price fluctuations, the value of the ladder as a whole may still be affected by changes in interest rates, economic conditions, or credit risk.
5. Complexity: Constructing and managing a bond ladder requires careful planning and monitoring, which may be daunting for inexperienced investors or those lacking time or expertise.
Difference Between Bond Ladder And Corporate Bond Ladder
| Comparison Terms | Bond Ladder | Corporate Bond Ladder |
|---|---|---|
| Scope of Bonds | A bond ladder includes various types of bonds such as government bonds, municipal bonds, and corporate bonds. | A corporate bond ladder specifically focuses on purchasing corporate bonds issued by corporations. |
| Issuer Type | Bonds in a bond ladder can be issued by governments, municipalities, or corporations. | Bonds in a corporate bond ladder are exclusively issued by corporations. |
| Risk Profile | The risk profile of a bond ladder depends on the mix of bonds it includes, spanning various issuers and sectors. | A corporate bond ladder may have a higher credit risk compared to a generic bond ladder, as it exclusively comprises corporate bonds subject to issuer-specific credit risk. |
| Market Dynamics | The performance of a bond ladder can be influenced by general market conditions, interest rate movements, and economic factors. | The performance of a corporate bond ladder may be more sensitive to company-specific factors such as financial health, industry trends, and credit ratings. |
| Income Characteristics | Bonds in a bond ladder provide income through periodic interest payments, with varying yields based on bond type and prevailing interest rates. | Corporate bonds in a corporate bond ladder offer income in the form of periodic interest payments, potentially reflecting higher yields compared to government or municipal bonds due to higher credit risk. |
Example Of Bond Ladder
Following is an example of a bond ladder with a five-year duration:
Year 1: Purchase bonds with varying maturities, such as one-year, two-year, three-year, four-year, and five-year bonds. For simplicity, let's allocate 20% of the total investment to each bond, totaling 100%.
Year 2: As the one-year bond matures, reinvest the proceeds into a new five-year bond. This maintains the ladder's structure with bonds spread across one to five years. Repeat this process each year.
Year 3: The original two-year bond matures. Reinvest the proceeds into a new five-year bond.
Year 4: The original three-year bond matures. Reinvest the proceeds into a new five-year bond.
Year 5: The original four-year bond matures. Reinvest the proceeds into a new five-year bond.
By following this approach, the bond ladder is consistently replenished with new five-year bonds while maintaining exposure to various maturity dates.
Conclusion
A bond ladder is a vital tool for fixed-income investors, aiding in managing interest rate risk and securing steady income. Diversifying across bond maturities mitigates the impact of interest rate fluctuations, providing stability and flexibility aligned with varied investment goals.
Bond valuation and pricing are fundamental to understanding a bond ladder's efficacy.
This comprehension enables investors to optimize portfolio performance and income generation through systematic reinvestment of maturing bonds, ensuring a continuous cash flow stream for long-term financial sustainability.
The bond ladder strategy empowers investors to navigate market dynamics effectively. With careful planning, monitoring, and adaptation, investors can enhance portfolio resilience, income consistency, and overall investment success.
Everything You Need To Master Valuation Modeling
To Help You Thrive in the Most Prestigious Jobs on Wall Street.
Free Resources
To continue learning and advancing your career, check out these additional helpful WSO resources:


or Want to Sign up with your social account?